Следствия производной линейной функции

Во-первых, . Это следует из наших выкладок просто в силу того, что мы подставили ; .

Далее, . Итак, производная от константы равна нулю.

Производная функции

Дальше рассмотрим производную функции .

В силу того что 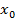– произвольна, имеем:

Где это может нам пригодиться? В дальнейшем с помощью производных мы будем исследовать свойства функций, говорить об их монотонности и т. д. Пока же мы можем говорить лишь о физическом и геометрическом смыслах. Разберем по примеру на каждый из них.

Пример 1

Тело движется по закону ( – в секундах, – в метрах). Какой будет скорость тела через 3 секунды после начала движения? Через какое время после начала движения скорость тела будет равна ?

Дано: , .

Найти: 1. , 2.

Прежде всего вспомним, что .

Отсюда мы можем вывести, что скорость через три секунды, то есть при , будет равна .

А скорость будет равна через 5 секунд ().

Ответ: , .

В качестве небольшого упражнения попробуйте сами вывести производную функции .

А сделав это, вы сможете решать физические задачи на равноускоренное движение. , где – ускорение.

Пример 2

В какой точке графика его касательная параллельна прямой ?

Дано: , .

Решение

Раз прямые параллельны, то их угловые коэффициенты равны, то есть угловой коэффициент касательной (он же тангенс угла наклона) должен быть равен 1. Но мы помним, что тангенс угла наклона касательной как раз равен производной в точке касания (в абсциссе точки касания) (см. рис. 1).

Рис. 1. Иллюстрация к примеру 1

Приравнивая имеем , значит, речь идет о касательной в точке .

Ответ: в точке .

Пример 3

Теперь рассмотрим кубическую функцию .

В силу того, что 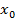произволен, имеем:

.

Итоги урока

На этом уроке мы с вами применяли определение производной на конкретных примерах. Мы вычислили производную линейной функции, производную и , а также пока без доказательства познакомились с производной от . Рассмотрели геометрический и физический смысл производной. Кроме этого, мы разобрали несколько примеров, увидели, где применяется производная.

Доказательство

.

По формуле бинома Ньютона:

Это доказательство верно только для натуральных , так как бином Ньютона работает только для натуральных .

Список литературы

1. Алгебра и начала анализа,  (в двух частях). Учебник для общеобразовательных учреждений (профильный уровень) / под ред. А.Г. Мордковича. – М.: Мнемозина, 2009.

2. Алгебра и начала анализа,  (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) / под ред. А.Г. Мордковича. – М.: Мнемозина, 2007.

3. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для  (учебное пособие для учащихся школ и классов с углубленным изучением математики) – М.: Просвещение, 1996.

4. А.Н. Колмогоров, А.М. Абрамов, Ю.П. Дудницын и др. Алгебра и начала анализа. Учеб. для 10-11 кл. – М.: Просвещение, 1990.