Непрерывность функции

Пример 1. Построить схематически графики функций:

1) , 2) ; 3) 4) 5)

и ответить на вопросы.

1. Сформулируйте определение функции, ее области определения и множества значений.

2. Определены ли функции в точке ?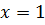

3. Является ли указанная точка внутренней точкой области определения?

4. Чем отличаются графики функций?

5. Имеют ли функции предел в точке 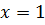? Если да, то чему он равен?

6. Равен ли предел значению функции в точке ?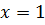

По ходу ответов на вопросы на наглядно-интуитивном уровне вводятся понятия функции непрерывной в точке и функции разрывной.

1. Если график функции в точке не «разрывается», то говорят, что функция в этой точке непрерывна (слово разрывается поставлено в кавычки, так как нами не определено точно, что значит разрывается).

2. Если график функции в точке «разрывается», то точка называется точкой разрыва функции, а о функции говорят, что она не является непрерывной в точке (является разрывной, терпит разрыв)

Ответив на все вопросы учитель вместе с учащимися дает строгое определение непрерывной функции в точке.

3. Введение понятия функции непрерывной в точке.

На этом этапе лекции формулируются два определения функции, непрерывной в точке.

Определение 1. Функция 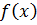, определенная в некоторой окрестности точки , называется непрерывной в точке , если .

Необходимо обратить внимание учащихся на то, что согласно данному определению непрерывность функции 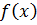в точке означает одновременную выполняемость следующих условий:

1. Функция 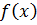должна быть определена в точке .

2. У функции 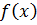должен существовать предел в точке . Как отмечалось выше, это подразумевает существование и равенство односторонних пределов в точке .

3. Предел функции 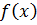в точке совпадает со значением функции в этой точке.

Прежде чем рассматривать второе определение функции, непрерывной в точке, необходимо вспомнить определение предела функции в точке и ввести понятия приращения аргумента и приращения функции .

Определение 2. Функция называется непрерывной в точке , если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции , то есть .

Приводятся примеры на использование определений 1 и 2 для доказательства непрерывности функции в точке.

Пример 2. Используя определение 1, доказать непрерывность функции в точке .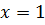

Пример 3. Используя определение 2, доказать непрерывность функции при любом значении .

Следует обратить внимание учащихся на то, что рассматривая аналогичным образом каждую основную элементарную функцию, можно доказать, что каждая основная элементарная функция непрерывна в каждой точке, в которой она определена.

4. Введение понятия односторонней непрерывности.

По аналогии с понятием предела слева и предела справа вводится понятие непрерывности слева и непрерывности справа. Можно предложить учащимся самостоятельно сформулировать эти определения.

Определение 3. Если функция 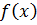определена на полуинтервале и , т.е. , то эта функция называется непрерывной справа в точке .

Определение 4. Если функция 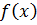определена на полуинтервале и , т.е. , то эта функция называется непрерывной слева в точке .

Необходимо обратить внимание учащихся на то, что для непрерывности функции в точке необходимо и достаточно её непрерывности в этой точке слева и справа.

В качестве примера можно рассмотреть одностороннюю непрерывность функций из примера 1.

5. Введение понятия функции непрерывной на отрезке

Формулируются определения функции непрерывной на интервале и функции непрерывной на отрезке.

Определение 5. Если функция непрерывна в каждой точке интервала 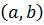, то она называется непрерывной на этом интервале.

Определение 6. Функция называется непрерывной на отрезке 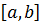, если она непрерывна на интервале 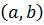и, кроме того, непрерывна справа в точке и непрерывна слева в точке .

Геометрический смысл введенных определений можно рассмотреть на примере функций из примера1.

6. Введение понятия точек разрыва и их классификации.

Формулируется определение точек разрыва и приводится их классификация.

Определение 7. Точка называется точкой разрыва функции 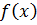, если эта функция либо не определена в точке , либо определена, но не является непрерывной в точке .

При этом следует отметить, что в точке разрыва нарушается одно из трех условий непрерывности. В зависимости от того какое условие нарушается выделяют точки разрыва первого рода (точки устранимого разрыва, точки разрыва с конечным скачком функции) и точки разрыва второго рода. У каждого типа разрыва есть свои характерные особенности, на которые нужно обратить внимание.

В качестве примера можно рассмотреть поведение вблизи точек разрыва графиков функций из примера 1.

7. Формулировка основных свойств функций, непрерывных в точке

Формулируются основные свойства функции, непрерывной в точке и даются указания на способы их доказательства.

1. Ограниченность в некоторой окрестности точки непрерывной в точке функции.

2. Знак функции, непрерывной в точке , в некоторой окрестности этой точки.

3. Непрерывность в точке суммы, произведения и частного непрерывных в точке функций.

4. Непрерывность сложной функции.

8. Формулировка основных свойств функций, непрерывных на отрезке

На этом этапе лекции формулируют без доказательства (доказательство теорем можно рассмотреть на семинаре) основные теоремы для функции, непрерывной на отрезке и рассматривают их геометрический смысл.

1. Теорема о нулях непрерывной на отрезке функции.

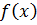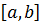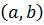Если функция определена и непрерывна на отрезке и принимает на его концах значения разных знаков, т.е. , то на интервале имеется по крайней мере один корень функции, т.е. .

2. Теорема о промежуточных значениях непрерывной на отрезке функции.

Если функция 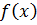определена и непрерывна на отрезке 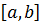и принимает на его концах различные значения , то для любого числа C, лежащего между A и B, на интервале 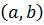найдется такая точка с, что .

3. Теорема об ограниченности непрерывной на отрезке функции.

Если функция 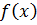непрерывна на отрез ке 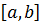, то она ограничена на этом отрезке.

4. Теорема о достижимости своего наименьшего и наибольшего значений функции, непрерывной на отрезке.

Если функция 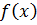непрерывна на отрезке 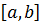, то она достигает на этом отрезке своего наибольшего и наименьшего значений.

Необходимо обратить внимание учащихся на значимость этих теорем для решения практических задач.

9. Подведение итогов

Проведение диагностической работы. Целью этой работы является определение уровня усвоения учебного материала, рассмотренного на лекции. Учащимся предлагается ответить на вопросы, сформулированные в начале лекции.

10. Постановка домашнего задания.

1. Разобраться с материалом лекции, выучить основные определения и формулировки теорем.

В результате этой лекции на рабочих листах, выданных в начале лекции, у учащихся появится опорный конспект.