Тема 3. Теоремы сложения и умножения вероятностей событий
Теорема умножения вероятностей независимых событий
Определение. Два события называются независимыми, если появление (или непоявление) одного из них не меняет вероятность появления другого события (или непоявления).
Пример.
1) Работа автоматических линий, которые не взаимосвязаны. А и В – остановки этих линий – независимые события.
2) Опыт состоит в бросании двух монет. События:  – появление герба на первой монете;
– появление герба на первой монете;  – появление герба на второй монете.
– появление герба на второй монете.
Заметим, что вероятность события  не изменяется, произошло ли событие
не изменяется, произошло ли событие  или нет. То же самое можно сказать и о вероятности события
или нет. То же самое можно сказать и о вероятности события  . События
. События  и
и  независимы.
независимы.
Теорема умножения вероятностей независимых событий
Вероятность произведения двух независимых событий равна произведению вероятностей этих событий:
 .
.
Задача. Вероятность того, что потребитель увидит рекламу определенного продукта по телевидению, равна 0,06. Вероятность того, что потребитель увидит рекламу того же продукта на рекламном стенде, равна 0,08. Предполагая, что оба события независимы, определить вероятность того, что потребитель увидит обе рекламы.
|
|
|
Решение.
Введем события:
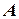 - потребитель увидит рекламу по телевидению;
- потребитель увидит рекламу по телевидению;
 - потребитель увидит рекламу на стенде;
- потребитель увидит рекламу на стенде;
 - потребитель увидит обе рекламы;
- потребитель увидит обе рекламы;
 - потребитель увидит хотя бы одну рекламу.
- потребитель увидит хотя бы одну рекламу.
События 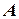 и
и  независимые.
независимые.
По условию задачи, вероятности  ;
;  .
.
Нужно найти вероятность  .
.
В наших обозначениях событие  - потребитель увидит две рекламы – это произведение событий
- потребитель увидит две рекламы – это произведение событий  . Поскольку события
. Поскольку события 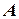 и
и  независимы, то
независимы, то  .
.
Ответ:  .
.
Зависимые события. Условная вероятность. Теорема умножения вероятностей зависимых событий
Определения.
Событие 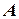 называется зависимым от события
называется зависимым от события  , если вероятность появления события
, если вероятность появления события 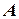 зависит от того, произошло или не произошло событие
зависит от того, произошло или не произошло событие  .
.
Вероятность того, что произошло событие 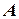 при условии, что произошло событие
при условии, что произошло событие  , будем обозначать
, будем обозначать  и называть условной вероятностью события
и называть условной вероятностью события 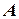 при условии
при условии  .
.
Пример. Пример зависимых событий.
В ящике 2 белых шара и 4 черных шара. Из ящика вынимают один шар (первое вынимание), затем второй шар (второе вынимание).
События:  – появление белого шара при первом вынимании;
– появление белого шара при первом вынимании;  – появление белого шара при втором вынимании.
– появление белого шара при втором вынимании.
Очевидно, что вероятность события  , если
, если  произошло, будет равна
произошло, будет равна
 .
.
Вероятность события  , если
, если  не произошло (при первом вынимании появился черный шар), будет равна
не произошло (при первом вынимании появился черный шар), будет равна
 .
.
Видим, что  .
.
Теорема умножения вероятностей зависимых событий
Вероятность произведения (совместного наступления) двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие произошло:
|
|
|
 или
или
 .
.
Задача. В ящике находится 12 деталей, из которых 8 стандартных. Рабочий берет наудачу одну за другой две детали, не возвращая первую в ящик. Найти вероятность того, что обе детали окажутся стандартными.
Решение. Введем следующие обозначения:
 – первая взятая деталь стандартная;
– первая взятая деталь стандартная;
 – вторая взятая деталь стандартная;
– вторая взятая деталь стандартная;
 - обе детали стандартные.
- обе детали стандартные.
Нужно найти вероятность  .
.
Вероятность того, что первая деталь стандартная, равна  .
.
Вероятность события  до того, как стало известно о качестве извлеченной первой детали, была равна 8/12. Наступление события
до того, как стало известно о качестве извлеченной первой детали, была равна 8/12. Наступление события  уменьшило общее число деталей в ящике (осталось 11) и число стандартных деталей (осталось 7) и, следовательно, изменило вероятность события
уменьшило общее число деталей в ящике (осталось 11) и число стандартных деталей (осталось 7) и, следовательно, изменило вероятность события  .
.
Вероятность того, что вторая взятая деталь окажется стандартной при условии, что первая деталь была стандартной (условная вероятность события  ) стала равной
) стала равной  . Событие
. Событие  зависит от события
зависит от события  .
.
Вероятность  того, что обе детали окажутся стандартными, находим по теореме умножения вероятностей зависимых событий:
того, что обе детали окажутся стандартными, находим по теореме умножения вероятностей зависимых событий:
 .
.
Вероятность появления трех зависимых событий:
 .
.
(… равна вероятности одного из событий на условные вероятности всех остальных событий при условии, что все предыдущие события уже наступили).
 2020-07-12
2020-07-12 194
194







