Геометрия Мора-Маскерони

Теория построения одним циркулем получила свою известность благодаря книге "Геометрия циркуля"(1797 г.) Лоренцо Маскерони³. Значительно позже в одном из букинистических магазинов была обнаружена книга датского математика Георга Мора "Датский Евклид", датированная 1672 годом! Обе книги содержат основной результат геометрии циркуля:

Теорема Мора-Маскерони. Все построения, выполненные с помощь циркуля и линейки, могут быть проделаны только с помощью циркуля (при этом мы считаем прямую построенной, если найдены хотя бы две точки этой прямой).

Для доказательства этой теоремы достаточно научиться находить только с помощью циркуля пересечения двух прямых, прямой и окружности, что и составляет проблему D. Сначала рассмотрим решения задач B и C, которые носят вспомогательный характер.

Решение B. Чтобы разделить отрезок [AB] на n равных частей, сначала увеличим его в n раз, т.е. найдем точку C, что |AC| = n|AB|. А затем построим точку C¢ - образ точки C при инверсии относительно окружности w(A,|AB|). Из соотношения |AC|·|AC¢| = |AB|² получаем |AC¢| = |AB|/n. Все указанные построения можно выполнить только с помощью циркуля (для этого даже не нужна прямая (AB)).

Решение C. Выберем произвольную точку O окружности w₁(X,r), центр X которой нам нужно определить (рис. 8).

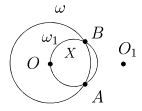
Рис. 8

Из точки O проведем произвольную окружность w(O,R) так, чтобы она пересекала исходную окружность w₁. Обозначим точки пересечения wÇw₁ через A и B. Куда перейдет прямая (AB) при инверсии inv_O^R? Конечно же в w₁, поскольку точки A и B остаются неподвижными (свойства II и VI). По свойству VII центр inv_O^R((AB)) (т.е. центр w₁) является образом точки S_(AB)(O) при inv_O^R. Из этих рассуждений следует цепочка необходимых построений. Сначала находим точку O₁ = S_(AB)(O), симметричную O относительно прямой (AB) (школьная задача). А затем строим образ точки O₁ при inv_O^R, он и будет искомым центром. Все указанные построения выполняются только с помощью циркуля.

Решение D. Опишем поиск пересечения двух прямых только с помощью циркуля. Пусть даны точки A, B, C и D (рис. 9).

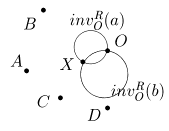
Рис. 9

Выберем точку O так, чтобы она не лежала на прямых a = (AB) и b = (CD). При инверсии inv_O^R прямые a и b должны перейти в окружности inv_O^R(a) и inv_O^R(b), а их точка пересечения отобразится в точку пересечения окружностей inv_O^R(a) и inv_O^R(b), отличную от точки O (свойства VI и I). Теперь необходимые построения становятся очевидными: с помощью свойства VII строим окружности inv_O^R(a) и inv_O^R(b), находим точку пересечения этих окружностей - точку X, и снова действуем инверсией уже на точку X. Точка Y = inv_O^R(X) является искомой. Пересечение прямой и окружности находится похожим образом.

Теперь терема Мора-Маскерони следует из решений задач B, C и D.

Задача Аполлония

В этом параграфе рассмотрим задачу о построении окружности, касающейся трех данных окружностей, названную в честь крупнейшего специалиста по коническим сечениям древности Аполлония Пергского⁴. Решению проблемы G предшествуют решения задач E и F.

Решение E. Чтобы построить окружность w₂, проходящую через точки A и B и касающуюся данной окружности w₁, рассмотрим инверсию с центром в точке O = A относительно окружности произвольного радиуса R. Образом w₂ при инверсии inv_O^R должна быть некоторая прямая a, проходящая через точку B¢ = inv_O^R(B) и касающаяся окружности inv_O^R(w₁) (свойства VIII и IX). Касательные из произвольной точки X к произвольной окружности w(Y,r) провести довольно легко: для этого достаточно построить вспомогательную окружность w¢ на диаметре [XY] и соединить X с точками пересечения wÇw¢. Теперь выполняем необходимые построения в следующем порядке: находим B¢ = inv_O^R(B) и inv_O^R(w₁), через точку B¢ проводим касательные a и b к окружности inv_O^R(w₁), строим образы inv_O^R(a) и inv_O^R(b) при инверсии inv_O^R. В зависимости от расположения точки B¢ относительно окружности inv_O^R(w₁) может быть два, одно и ни одного решения (например, когда B¢ находится внутри inv_O^R(w₁)).

Решение F. Для решения этой задачи достаточно уметь проводить общую касательную к двум произвольным окружностям w(X,r) и w¢(Y,R). Будем считать, что r < R. Проведем из точки X касательную a к окружности w₁(Y,R-r) (рис. 10), тогда искомая внешняя касательная b к окружностям w и w¢ будет параллельна прямой a и находится от нее на расстоянии r.

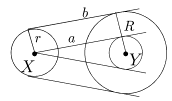
Рис. 10

Для проведения внутренней касательной вместо w₁(Y,R-r) надо рассмотреть окружность w₂(Y,R+r). В общем случае возможно до четырех решений. Теперь вернемся к исходной задаче. Пусть даны точка A и две окружности w₁ и w₂. Искомая окружность w, проходящая через A и касающаяся w₁ и w₂, при инверсии с центром O = A должна перейти в некоторую прямую a, которая касается окружностей inv_O^R(w₁) и inv_O^R(w₂) (свойства VIII и IX). Таким образом, приходим к следующему порядку построений: находим inv_O^R(w₁) и inv_O^R(w₂), проводим общие касательные (a,b,c,d) и строим образы этих касательных при inv_O^R. В общем случае получится до четырех искомых окружностей, однако в одном случае решений будет бесконечно много (представьте, что произойдет после инверсии с окружностями w₁ и w₂, если они касаются в точке A).

Решение G. Задача Аполлония легко сводится к предыдущей задаче. Пусть даны окружности w₁(O₁,r₁), w₂(O₂,r₂) и w₃(O₃,r₃), и r₁ < r₂ < r₃. Построим окружность w(O,R), проходящую через точку O₁ и касающуюся окружностей

w₂(O₂,r₂-r₁) и w₃(O₃,r₃-r₁). Уменьшив радиус окружности w на r₁, т.е. рассматривая w(O,R-r₁), приходим к одной из искомых окружностей. Количество решений исследовать самим (кажется, исключая бесконечный случай, возможно до восьми решений).