Симметрическая группа

Симметрической группой множества 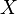называется группа всех перестановок 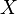(то есть биекций ) относительно операции композиции.

Симметрическая группа множества 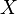обычно обозначается . Если , то также обозначается через 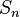. Но если , то изоморфна , потому при конечном считают, что равно .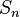

Нейтральным элементом в симметрической группе является тождественная перестановка , определяемая как тождественное отображение:

для всех .

Свойства

• При симметрическая группа 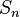некоммутативна.
• При симметрическая группа 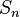является неразрешимой (и напротив: при — разрешимой).
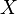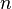• В случае, если конечно, число элементов равно (факториал n), где — число элементов 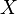. В частности,
• Каждая конечная группа изоморфна некоторой подгруппе группы (Теорема Кэли).
• Симметрическая группа 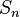допускает следующее задание:

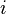(Можно считать, что переставляет и .)

• Максимальный порядок элементов группы 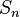- функция Ландау.
• центр симметрической группы тривиален при .
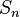• Симметрическая группа является совершенной (то есть группа её автоморфизмов совпадает с самой группой) тогда и только тогда, когда ее порядок отличен от 2 и 6 (теорема Гёльдера). В случае группа имеет еще один внешний автоморфизм. В силу этого и предыдущего свойства при все автоморфизмы являются внутренними, то есть каждый автоморфизм имеет вид для некоторого .
• Число классов сопряженных элементов симметрической группы 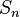равно числу разбиений числа n. ^[2].
• Множество транспозиций является порождающим множеством 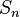. С другой стороны, все эти транспозиции порождаются всего двумя перестановками , так что минимальное число образующих симметрической группы равно двум.
• Знакопеременная группа 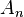является нормальной подгруппой 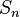. Причем 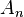- единственная нормальная подгруппа 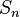, а при имеет еще одну нормальную подгруппу - четверную группу Клейна.