Вычисление периода одномерных колебаний

Одномерное финитное движение всегда является колебательным. Частица совершает периодически повторяющиеся движения между двумя точками остановк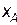и и . При этом время движения от 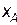к 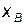и обратно, от 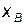к 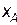одно и тоже и равно половине периода колебаний. Выберем за начало отсчета времени тот момент, когда частица находилась в крайней левой точке . Тогда

(18)

Координаты точек остановки и , определяемые из уравнения (17), зависят от энергии .

Рассмотрим простой пример. Вычислим с помощью формулы (18) период и собственную частоту гармонических колебаний тела на пружине жесткостью , если задана энергия системы .

Т.к. потенциальная энергия пружины , то формула (18) принимает вид:

Точки остановки и . Делая замену переменной интегрирования , приводим интеграл к виду

В результате имеем: .

Видим, что в поле , период колебаний не зависит от энергии системы. Не трудно сообразить, что амплитуда колебаний зависит от энергии и определяется по формуле: .

9.Движение двух взаимодействующих частиц. Приведение к задаче о движении в центральном поле.

Полное аналитическое решение в общем виде допускает чрезвычайно важная задача о движении системы из взаимодействующих друг с другом двух тел массами и . Это, так называемая, задача «двух тел».

Проще всего решать эту задачу в системе центра масс (Ц -системе). Однако, для большей наглядности мы начнем её решение в лабораторной системе (Л -системе), переходя затем в Ц -систему. Это позволит нам на языке уравнений Лагранжа наглядно продемонстрировать преимущества Ц -системы.

Рассматриваемая механическая система двух тел система имеет 6 степеней свободы: . Обозначим радиус-вектора частиц в Л -системе и (см. рисунок). Тогда функция Лагранжа в Л -системе будет иметь вид:

(1)

Шесть уравнений Лагранжа и двенадцать начальных условий в Л-системе имеют обычный вид:

(2)

Т.к. система замкнута, что её полный импульс сохраняется:

; где (3)

Поскольку потенциальная энергия взаимодействия частиц зависит только от расстояния между частицами, то с учетом формулы (3), удобно от пары векторных переменных и перейти к новым переменным и (См. рисунок):

и (4)

Из формул (4) находим связь между старыми и новыми переменными:

(5)

Величина есть не что иное, как центр инерции системы: . Величина определяет относительное расположение частиц друг относительно друга.

В Ц -системе, радиус-вектор каждой из частиц и будет определяться по формулам:

(6)

Переход к новым переменным, фактически, представляет движение механической системы из двух тел как движение её как целое (переменная ) и движение каждой из частиц относительно их общего центра инерции (переменные и ).

Дифференцируя уравнения (5) по времени и подставляя полученные производные в выражение для функции Лагранжа системы (1), получим

(7)

где введено обозначение

(9)

Величина (9) называется приведенной массой двух тел. Функция Лагранжа (7) в новых переменных состоит из двух слагаемых: первое зависит только от величины , причем радиус вектор центра инерции является циклической переменной. Второе слагаемое зависит только от величин и , и только в него входит потенциальная энергия взаимодействия 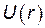. Но это означает, что в новых переменных уравнения Лагранжа для величин и будут независимыми – закон относительного движения частиц никак не связан с движением центра инерции системы .

Из формулы (7) получаем уравнения Лагранжа системы двух тел

(10)

Уравнения (10) означают, что, во-первых, центр инерции системы движется равномерно и прямолинейно, а, во вторых, относительное движение тел таково, каким было бы движение тела с приведенной массой в потенциале .

Таким образом, для того чтобы определить положение каждой из двух частиц, как в Л -системе, так и в Ц -системе, остается определить зависимость от времени только их относительного движения, т.е. величины .

Таким образом, переход в Ц – системе позволяет задачу с шестью степенями свободы, свести к более простой задаче с тремя степенями свободы. Поэтому следующий шаг состоит в том, чтобы получить уравнение непосредственно для величины . Поэтому становится актуальной проблема изучения движения одной м. точки в заданном внешнем Ц.С. поле . Эта задача в общем виде будет рассматриваться в следующей лекции; сейчас же в связи со вторым уравнением (10) рассмотрим вопрос о силах, которые действуют на частицу в центрально-симметричном поле.

Если потенциальная энергия частицы зависит только от расстояния до определенной неподвижной точки, которая называется центром поля, то на частицу со стороны поля действует сила

(11)

Эта сила по абсолютной величине зависит только от расстояния до центра поля и направлена в каждой точке коллинеарною радиус-вектору . Если , то в данной точке это сила отталкивания . Если , то в данной точке это сила притяжения . Важнейшими ЦС полями являются: гравитационное поле двух точечных масс (закон всемирного тяготения Ньютона) и электростатическое поле двух точечных зарядов (закон Кулона):

; .

Гравитационное поле может быть только полем притяжения . Кулоновское поле может быть как полем притяжения так и полем отталкивания , причем первый случай реализуется при разноименных зарядах движущейся частицы и центра поля, второй – в случае, когда эти заряды одноименные.

10. Общие закономерности движения в центральном поле. Интегралы движения. Интегрирование уравнений движения

Выберем начло координат в центре поля (См. рисунок). В начальный момент времени частица находилась в како-то точке , имела импульс и, следовательно, имела относительно центра поля момент импульса . Как нам уже известно, при движении в ЦС поле сохраняется момент импульса относительно центра поля:

(1)

Следовательно, в каждый момент в ремени величины и . Поэтому из закона сохранения момента импульса сразу следует, что траектория движение частицы в ЦС всегда остается в одной плоскости, перпендикулярной . Но это означает, что рассматриваемая задача имеет две степени свободы: s=2, а общее решение уравнений движения должно содержать четыре произвольные константы.Выберем ось вдоль вектора , так, что

, т.е. (2)

При таком выборе оси движение частицы будет происходить в плоскости . (см. рисунок).

Используем далее полярные координаты и . В полярных координатах ф. Лагранжа имеет известный нам вид:

(3)

Уравнения Лагранжа будут выглядеть так:

; (4)

; (5)

Поскольку ф. Лагранжа не зависит явно от угла , то координата является циклической. Поэтому из уравнения Лагранжа (5) сразу следует, что сохраняется обобщенный импульс: . Как нам известно, величина . Но при нашем выборе осей координат . Поэтому уравнение (5) выражает закон сохранения момента импульса относительно центра поля:

(6)

Закон сохранения момента при плоском движении допускает наглядную геометрическую интерпретацию. Выражение есть площадь сектора, образованными двумя бесконечно близкими радиус-векторами с углом между ними и элементом дуги траектории. Поэтому закон сохранения момента импульса (6) можно записать в виде:

(7)

Производную называют секториальной скоростью, а закон сохранения момента импульса иногда называется интегралом площадей: за равные промежутки времени радиус-вектор движущейся точки описывает равные площади (второй закон Кеплера).

Из формулы (6) получаем, что

(8)

Следовательно, угол монотонно возрастает со временем, т.е. угловая скорость частицы . Из (8) сразу следует, что наибольшее значение угловая скорость достигает при наименьшем расстоянии частицы от центра поля:

(9)

Полное решение задачи о движении в ЦС проще всего получить, используя законы сохранения энергии и импульса:

(10)

Из второго уравнения (10) сразу находим угловую скорость

(11)

Подставляя (11) в первое уравнение (10) получаем:

(12)

Здесь - так называемая «эффективная» потенциальная энергия частицы в ЦС поле:

(13)

Величину называют центробежной энергией. Соответствующая её центробежная сила всегда является силой отталкивания:

. (14)

Только в тех случаях, когда , величина эффективной потенциальной энергии совпадает с истинной потенциальной энергией частицы:

(15)

Уравнение (12) для радиального движения частицы формально похоже на одномерное уравнение движение частицы с одной степенью свободы, изученное нами ранее. Однако следует помнить, что в рассматриваемой задаче величина всегда положительна: и точка является центром поля. Кроме того, если , то это не точка остановки, как при истинном одномерном движении, а точка остановки радиального движения. Границы области движения (по расстоянию от центра) определяются условием:

(16)

Уравнение

(17)

определяет минимальное и максимальное расстояния от частицы до центра поля. Следует обратить внимание на то обстоятельство, что величины и зависят от и , как от параметров рассматриваемой задачи. Из уравнения (12) сразу находим, что

(18)

Разделяя переменные, получаем:

(19)

Формула (19) определяет (в неявном виде) зависимость расстояния от частицы до центра поля в любой момент времени . Переписав уравнение (11) и (18) в виде

, ,

получаем уравнение траектории:

(20)

Здесь - начальный азимутальный угол. Формула (20) определяет уравнение траектории частицы в плоскости в полярных координатах. Таким образом, формулы (19) и (20) полностью решают задачу о движении частицы в произвольном ЦС поле . вся сложность решения такого рода задач смещается из плоскости физической в математическую плоскость.

11. Общие закономерности движения в центральном поле.Финитное и инфинитное движение. Падение на центр

Из уравнения (17) находим точки поворота. Если это уравнение имеет всего один корень , то движение частицы инфинитно: её траектория, начинаясь в точке , пройдет через некоторое время точку наибольшего сближения и затем уйдет на бесконечность. Если уравнение (17) имеет два корня и , то движение частицы финитно. В этом случае траектория частицы целиком лежит внутри кольц а , ограниченного окружностями и .

Но это вовсе не означает, что при финитном движении траектория частицы непременно является замкнутой кривой. За время, в течение которого расстояние изменяется от величины до и обратно до , радиус вектор повернется на угол (согласно формуле (20)) на величину

. (21)

Условие замкнутости траектории выражается условием: . Тогда, через повторений периода времени радиус вектор точки, сделав полных оборотов, совпадет со своим первоначальным значением, т.е. траектория замкнется. Можно строго показать, что такая ситуация возможна только для двух потенциалов: (задача Кеплера) и (пространственный осциллятор).

В заключение этого раздела рассмотрим вопрос о возможности падения частицы на центр поля, когда поле носит характер притяжения.

Сначала рассмотрим простейший случай, когда . Это будет иметь место, когда либо начальная скорость равна нулю (), либо когда вектор коллениарен вектору . Понятно, что во всех этих случаях движение будет прямолинейным: - это уравнение прямой в полярных координатах.

Если или , то падение на центр неизбежно. Если же начальная скорость направлена от центра, то возможны два случая:

1. Уравнение не будет иметь решения при . Тогда частица удалится на бесконечность.

2. Уравнение будет имеет корень . Тогда траектория частицы будет состоять из двух частей. На первом участке частица будет удаляться от центра до расстояния . В точке частица, имея нулевую скорость, под действием сил притяжения начнет двигаться в обратную сторону и в конечном итоге упадет на центр поля притяжения.

Наконец рассмотрим вопрос о возможности падения на центр в общем случае, когда . Наличие центробежной энергии, стремящейся при к по закону , делает обычно невозможным проникновения частиц к центру поля, даже если это поле притяжения. Теоретически, падение на центр возможно лишь тогда, если достаточно быстро стремиться к при . Перепишем условие, определяющее область допустимых расстояний, в виде:

(22)

Необходимо, чтобы это условие выполнялось вплоть до точки . Полагая в последней формуле , запишем её так:

(23)

Здесь учтено, что при , величина , независимо от значения полной энергии . Последнее неравенство может выполняться в двух случаях:

1. Если , при (24)

2. Если , при (25)

Конечно, полученные ограничения на вид потенциальной энергии, означают только, что при их выполнении падение частицы на центр возможно в принципе, т.е. они являются необходимыми условиями падения на центр поля. Но их выполнение вовсе не означает, что в процессе движения частица достигнет центра поля. Это зависит от начальных условий. Например, начальные условия в любом центральном поле можно выбрать так, чтобы частица вращалась по окружности вокруг центра поля. В этом случае падения на центр поля не будет, даже если установленные выше условия будут выполнены.

12. Движение в кулоновском поле притяжения. Уравнения траекторий и классификация орбит

Рассмотрим движение частицы массы во внешнем поле

; (1)

когда

Это соответствует полю притяжения, т.е., так называемую задачу Кеплера. Будем считать, что начальный радиус - вектор и начальный импульс лежат в плоскости . Тогда движение частицы будет происходить только в этой плоскости

Направим ось так, чтобы она совпадала с направлением вектора . Тогда будем иметь, что . Отсюда следует, что и, следовательно, , где - значение азимутального угла при .

Эффективная потенциальная энергия в рассматриваемом поле (1)

(2)

Если , то и движение будет происходить по прямой: . В этом простейшем случае, величина эффективной потенциальной энергии (2) совпадает с реальной потенциальной энергией. Этот случай сводится к одномерному движению, поэтому далее мы будем предполагать, что . В этом случае азимутальный угол будет монотонновозрастать со временем: .

Исследуем подробно зависимость для случая . При величина по закону . при величина со стороны отрицательных значений по закону .

В точке

, (3)

величина имеет локальный минимум:

, (4)

В точке

, (5)

график функции обращается в ноль: Другими словами, график зависимости , имеет вид «потенциальной ямы».

Таким образом, значение величины определяет как положение точки минимума, так и расстояние, на котором , т.е. определяет основные параметры эффективной потенциальной энергии. Поэтому, величину называют параметром орбиты. В поле притяжения величина всегда положительнаи определяется моментом импульса .

С учетом (5) выражение для величины можно записать в виде:

(6)

Из формулы (6) видно, что величина играет роль характерной длины в данной задаче. Поэтому удобно измерять расстояние до центра в единицах , которое мы будем обозначать буквой (приведенное расстояние):

(7)

В терминах приведенных расстояний, формулу (6) можно записать в виде:

(8)

Из формулы (8) следует, что имеет минимум при . Из предыдущей лекции нам известно, что область допустимых расстояний до центра поля, где может происходить движение частицы, определяется из уравнения . В нашем случае, используя выражение (8), получаем:

(9)

Решение уравнения (9), квадратного относительно переменной , дает:

(10)

Величина в формуле (10) определяется выражением:

(11)

Величина называется эксцентриситетом орбиты.

Параметр орбиты, может быть определен всегда, при заданном значении . Что касается эксцентриситета орбиты, то величина может быть рассчитана только в том случае, когда выполняется неравенство:

, т.е. (12)

Полная механическая энергия может быть как положительной, так и отрицательной или равной нулю, в зависимости от начальных значений и :

(13)

Если энергия частицы не отрицательна (), то неравенство (12) выполняется автоматически. В этом случае эксцентриситет орбиты всегда больше или равен единицы:

(14)

Поэтому в формуле (10) можно брать только знак «+», т.к. в противном случае дробь будет отрицательной. Но это означает, что при уравнение имеет только один положительный корень:

(15)

Из формулы (15) видно, что при . Т.о., в этом случае имеется толькоодна точка поворота и движение частицы будет инфинитным в области расстояний от центра поля: .

Теперь рассмотрим противоположный случай, когда энергия частицы отрицательна: . В этом случае неравенство (12) будет выполняться не всегда, а только в том случае, если величина энергии частицы удовлетворяет условию

; (16)

В этом случае эксцентриситет орбиты

(17)

меньше единицы и изменяется в пределах:

Это означает, что при уравнение имеет два корня: и :

и (18)

Следовательно, движение частицы финитно, и происходит в области расстояний до центра поля

(19)

Из формулы (19) видно, что эксцентриситет определяет степень “вытянутости” орбиты. Если то орбита сильно вытянута, т.к. , а . Наоборот, если , то и и . Если энергия частицы определяется формулой

(20)

то . Следовательно, частица все время находится на одном и том же расстоянии от центра, т.е. вращается по окружности, радиуса

(21)

Здесь - начальное расстояние частицы от центра поля при .

Итак, мы выполнили предварительный анализ характера траектории частицы. Мы выяснили, при каких значениях энергии движение будет инфинитным, финитным и даже определили условия, при которых траектория финитного движения будет окружностью. Мы вычислили скорость вращения по окружности при заданном начальном расстоянии от центра . Теперь проведем анализ возможных траекторий движения в задаче Кеплера.

13. Движение в кулоновском поле притяжения (задача Кеплера). Классификация орбит при финитном и инфинитном движении

В предыдущей лекции мы выяснили, при каких значениях энергии движение будет инфинитным, финитным, а так же определили условия, при которых траектория финитного движения будет окружностью. Мы вычислили скорость вращения при заданном начальном расстоянии от центра . Теперь, проведя общее исследование возможных особенностей движения, получим уравнения траекторий движения частицы в поле притяжения . Получим уравнения возможных траекторий частицы.

Будем использовать полученное ранее выражение для зависимости , которое фактически уже определяет траекторию движения в неявном виде. Напомним, что

(1)

Для определения вида траектории (а не самого закона движения), совершенно не важен выбор знака перед интегралом в формуле (1). Кроме того, в астрономии принято выбирать так, чтобы в начальный момент времени, тело находилось на наименьшем расстоянии от центра, т.е. в перигелии орбиты. С учетом сказанного, выражение (1) для нашей конкретной задачи, можно записать в виде:

. (2)

Используя выражения для параметра и эксцентриситета, введенные в предыдущей лекции, получим:

(3)

Здесь, как и ранее, - безразмерное расстояние до центра поля и . Осуществляя в (3) замену переменной интегрирования: , , приводим интеграл к табличному виду:

Поэтому получаем:

Легко видеть, что второе слагаемое равно нулю. Поэтому:

(4)

Откуда

(5)

Это и есть уравнение семейства траекторий в поле притяжения в полярных координатах.

Теперь приступим к анализу выражения (5) для различных значений энергии частицы . Проведем анализ различных траекторий движения в задаче Кеплера, записав уравнение (9.6)

, (6)

в обычных декартовых координатах. Учитывая, что , запишем , т.е.

(7)

Это и есть уравнение траекторий в декартовых координатах.

Рассмотрим сначала случай финитного движения, когда энергия отрицательна: . В этом случае эксцентриситет орбиты . Перепишем уравнение (7) в виде

(8)

Отсюда видно, что уравнение траектории при финитном движении принимает канонический вид:

(9)

Это есть уравнение эллипса с полуосями и с началом координат в точке :

. . (10)

Поскольку , то . Большую полуось эллипса можно было сразу определить из уравнения: . Отсюда получаем, что

(11)

Таким образом, большая полуось эллипса зависит только от энергии частицы. При получаем уравнение окружности с радиусом .

Таблица 9.1

В таблице 9.1 приведены значения нескольких характерных точек траектории при финитном движении, рассчитанные по полученным выше формулам.

На рис.1 представлены орбиты движения частицы в поле притяжения при финитном движении для различных значений эксцентриситета , рассчитанные по формуле (9) в приведенных единицах . Видно, что все орбиты имеют две общие точки при , когда .

Рис.1 Орбиты при финитном движении частицы при различных

эксцентриситетах орбиты

Чтобы вычислить время обращения по эллиптической орбите, т.е. период обращения воспользуемся законом сохранения момента импульса:

где - площадь сектора орбиты. Интегрируя это равенство по , получим, что , где - площадь эллиптической орбиты: . Подставляя сюда значения и из (9.17), будем иметь:

(12)

Заметим, что период зависит только от энергии частицы.

Теперь рассмотрим случай инфинитного движения, когда энергия положительна: . В этом случае эксцентриситет орбиты .

Рассмотрим сначала самый простой случай, когда энергия частицы , т.е. . В этом случае уравнение (7) принимает вид:

, (13)

Уравнение (13) есть уравнение параболы в области (красная кривая на рисунке 2.

Если , т.е. , то уравнение траектории в декартовых координатах будет иметь вид:

(14)

Здесь

, , (15)

Уравнение (15) есть уравнение гиперболы, с «полуосью» .

На рис.2 представлены орбиты движения частицы в поле притяжения при инфинитном движении для различных значений эксцентриситета в приведенных единицах .

Рис.9.2 Орбиты при инфинитном движении частицы

при различных эксцентриситетах орбиты.

При () траекториями движения являются гиперболы, огибающие центр поля (фокус) – черная и синяя кривые. При значение и траекторией движения является парабола – красная кривая. Видно, что, как и при финитном движении, все орбиты имеют две общие точки при , когда .