С постоянными коэффициентами

Линейное дифференциальное уравнение (ЛДУ) второго порядка с постоянными коэффициентами имеет вид

                                       ,                                   (7.7)

где  и  – действительные числа,  – некоторая функция.

Если , то уравнение

                                                                           (7.8)

называется однородным; в противном случае при  уравнение (7.7) называется неоднородным.

Структура общего решения ЛДУ второго порядка определяется следующей теоремой:

Теорема 7.1.   Общее решение неоднородного уравнения (7.7) представляется как сумма какого-нибудь частного решения  этого уравнения и общего решения  соответствующего однородного уравнения (12.8):

                                             .                                             (7.9)

Рассмотрим сначала решение линейного однородного уравнения (7.8) с постоянными коэффициентами.

Составим для линейного однородного ДУ характеристическое уравнение (для этого достаточно в уравнении (7.8) заменить  и  соответственно на  и 1):

                                             .                                          (7.10)

При решении характеристического уравнения возможны следующие три случая.

Случай 1. Корни характеристического уравнения действительные и различные: , , . Тогда общее решение уравнения (12.8) имеет вид

                                          .                                      (7.11)

Случай 2. Корни характеристического уравнения действительные и равные: , . Тогда общее решение уравнения (12.8) имеет вид

                             .                   (7.12)

Случай 3. Корни характеристического уравнения комплексные: , . Тогда общее решение уравнения (12.8) имеет вид

                              .                      (7.13)

 Таким образом, нахождение общего решения ЛОДУ второго порядка с постоянными коэффициентами (7.8) сводится к нахождению корней характеристического уравнения (7.10) и использованию формул (7.11) – (12.13) общего решения уравнения (не прибегая к вычислению интегралов).

Перейдем теперь к решению линейного неоднородного дифференциального уравнения (ЛНДУ) второго порядка с постоянными коэффициентами (7.7).

Суть метода, называемого методом неопределенных коэффициентов, состоит в следующем: по виду правой части  уравнения (7.7) записывают ожидаемую форму частного решения с неопределенными коэффициентами, затем подставляют ее в уравнение (7.7) и из полученного тождества находят значения коэффициентов.

Случай 1. Правая часть уравнения имеет вид , где  – многочлен степени . Уравнение (7.7) запишется в виде

.

В этом случае частное решение ЛНДУ  ищем в виде

                                        ,                                     (7.14)

где  – многочлен степени , записанный с неопределенными коэффициентами , а  – число совпадений  с корнями  характеристического уравнения (7.10).

Случай 2. Правая часть уравнения имеет вид

,

где  и  – многочлены степени  и  соответственно,  и   – действительные числа. Уравнение (7.7) запишется в виде

             .    (7.15)

В этом случае частное решение следует искать в виде

                  ,        (7.16)

где   – число совпадений  с корнями  характеристического уравнения (7.10),   и  – многочлены степени  с неопределенными коэффициентами,  – наивысшая степень многочленов  и , т.е. .

Замечание 1.  После подстановки функции (7.16) в уравнение (7.15) приравнивают многочлены, стоящие перед одноименными тригонометрическими функциями в левой и правой частях уравнения.

Замечание 2. Форма (7.16) сохраняется и в тех случаях, когда  или .

 

 

РЯДЫ

Числовые ряды

Под числовым рядом понимают всякое выражение вида

                              (8.1)

где  числа, называемые членами ряда (  называют первым членом ряда,  – вторым членом ряда, и т. д.). -й член ряда называют также общим членом ряда. Сокращенно ряд (8.1) обозначают следующим образом:

Ряд (8.1) считается заданным, если известен закон, по которому можно вычислить его член  для любого номера

Сумма первых  членов ряда (8.1) называется 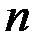- йчастичной суммой данного ряда и обозначается  то есть

Пусть задан ряд (13.1). Рассмотрим его частичные суммы

Они образуют числовую последовательность { }.

Если существует конечный предел  последовательности частичных сумм ряда (8.1) (), то говорят, что ряд (13.1) сходится, В этом случае  называют суммой ряда (13.1). Записывают:

Если последовательность частичных сумм ряда (8.1) не имеет конечного предела, то говорят, что ряд (8.1) расходится.

Теорема 8.1. Если сходится ряд, получившийся из данного ряда (8.1) отбрасыванием нескольких его членов, то сходится и сам данный ряд. Обратно, если сходится данный ряд, то сходится и ряд, получившийся из данного отбрасыванием нескольких членов.

Теорема 8.2. Если ряд (8.1) сходится и его сумма равна  то ряд

где  – какое-либо фиксированное число, также сходится и его сумма равна

Теорема 8.3. Если ряды

и

сходятся и их суммы, соответственно, равны  и  то ряды

и

также сходятся и их суммы, соответственно, равны

Необходимый признак сходимости числового ряда. Если ряд (8.1) сходится, то его общий член  стремится к нулю при

Отсюда следует достаточное условие расходимости числового ряда: если  или этот предел не существует, то ряд расходится.

Замечание 8.1. Из того, что -й член ряда (8.1) стремится к нулю при  еще не следует, что этот ряд сходится, – ряд может и расходиться. Например, известно, что так называемый гармонический ряд

расходится, хотя