2020-10-12
134
Пусть функция 
задана на отрезке 
. Разобьем отрезок на 
– элементарных отрезков точками 
. В каждом из отрезков разбиения 
выберем произвольно точку 
и положим 
.
Сумма всех таких произведений
или короче: 
называется интегральной суммой для функции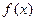 
на отрезке .
Пусть существует и конечен предел 
интегральной суммы при стремлении к нулю , не зависящей от способа разбиения отрезка на части и способа выбора точек 
на отрезках разбиения. Тогда функция называется интегрируемой на , число – определенным интегралом от 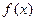на и обозначается 
; 
.
Рассмотрим свойства определенного интеграла.
Свойство 1. Если нижний и верхний пределы интегрирования равны (a = b), то интеграл равен нулю:
Свойство 2. Если f(x) = 1, то 
Свойство 3. При перестановке пределов интегрирования определенный интеграл меняет знак на противоположный:
Свойство 4. Постоянный множитель можно выносить за знак определенного интеграла:
R.
Свойство 5. Определенный интеграл от алгебраической суммы конечного числа интегрируемых на [a; b] функций f1(x), f2(x), …, fn(x) равен алгебраической сумме определенных интегралов от слагаемых:
Свойство 6. (аддитивность определенного интеграла). Если существует интегралы 
и 
то существует также интеграл 
и для любых чисел a, b, c;
Свойство 7. Если f(x) ≥ 0 
[a; b], то 
a < b.
Свойство 8. (определенность определенного интеграла). Если интегрируемые функции f (x) и φ (x) удовлетворяют неравенству f (x) ≥ φ (x) [a; b], то
a >b.
Свойство 9. (об оценке определенного интеграла). Если m и М – соответственно наименьшее и наибольшее значения функции f (x), непрерывной на отрезке [a; b], то 
a < b.
Свойство 10. (теорема о среднем). Если функция f (x) непрерывна на отрезке [a; b], то существует такая точка 
[a; b], что 
т.е. определенный интеграл от переменной функции равен произведению значения подынтегральной функции в некоторой промежуточной точке ξ отрезка интегрирования [a; b] и длины b – a этого отрезка.
