2020-10-12
140
Определение: Ряды, члены которых имеют чередующиеся знаки, называются знакочередующимися. Знакочередующийся ряд, если первый член положителен, можно записать в виде: 
, где 
, 
Признак Лейбница:
Если у знакочередующегося ряда абсолютные величины членов ряда убывают: 
и общий член стремится к нулю при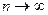 
, то ряд сходится.
Пример 11. Исследовать сходимость знакочередующегося ряда
1) 
Решение:
Члены ряда монотонно убывают по абсолютной величине:
и 
. Данный ряд сходится.
Пример 12. 
Решение:
Вместо данного ряда возьмём ряд, составленный из абсолютных величин данного ряда 
. Это ряд с положительными членами, сравним его по первому признаку сравнения с рядом 
; 
. Ряд – геометрическая прогрессия со знаменателем 
, он сходится. По признаку сравнения данный ряд сходится.
Пример 13. 
Решение:
По признаку Лейбница 
Первое условие признака Лейбница выполнено, т.е. второе условие
выполнено. Ряд сходится.
Определение: Ряд 
называется абсолютно сходящимся, если сходится ряд 
составленный из абсолютных величин его членов. Ряд называется условно сходящимся, если он сходится, а ряд расходится.
|
|
|
Пример 14. Ряд 
– абсолютно сходящийся, т.к. ряд, составленный из абсолютных величин сходится.
Пример 15. Ряд 
условно сходится. Оба условия признака Лейбница выполнены:
1) 
2) 
Ряд, составленный из модулей его членов 
, расходится по интегральному признаку сравнения. Деление сходящихся рядов на абсолютно и условно сходящиеся весьма существенно. Основные свойства конечных сумм переносятся только на абсолютно сходящиеся ряды, тогда как условно сходящиеся ряды некоторыми из этих свойств не обладают.
