Обоснование основных понятий комбинаторики

Комбинаторика.

Множества. Операции с множествами.

Лекция №7

План:

1. Элементы и множества.

2. Подмножества.

3. Операции над множествами и их свойства.

4. Обоснование основных понятий комбинаторики: факториал, перестановки, размещения, сочетания.

Элементы и множества.

Множество представляет собой соединение, совокупность, собрание некоторых элементов, объединенных по какому-то признаку. Например: множество учащихся группы, множество букв алфавита и т.д. В математике множество используется для описания математических понятий. Например: множество вершин данного многоугольника, множество натуральных чисел, множество точек данной прямой и т.д.

Обозначение множеств: (множества обозначают заглавными буквами латинского алфавита) A, B, C…..X, Y, …

Предметы, из которых состоит множество, называют его элементами и обозначают малыми буквами латинского алфавита: a, b, c, d…..

Например:

1. N = {1, 2, 3, 4…..} – множество натуральных чисел (задано перечислением)

1 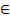N; 100 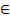N; 5,5 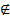N; 0 ∉ N.

2. М = {x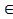N 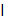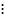2 } – множество натуральных чисел, делящихся на 2 (или множество четных натуральных чисел).

2 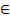М; 10 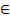М; 3 ∉ М.

Обычно множество задается указанием характеристического свойства его элементов, т.е. такого свойства, которым обладают все элементы данного множества и только они.

Чаще всего это свойство формулируется словестно. Например: множество решений уравнения х² – 1 = 0; множество точек плоскости, равноудаленных от данной точки.

Может оказаться, что множество определено таким свойством, что которым не обладает вообще ни один объект. Говорят, что эти множества пустые. Обозначают: .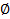

Например:

Множество решений системы уравнений:

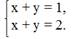
Множества, состоящие из одних и тех же элементов, называются равными. Обозначают: А = В.

Например:

Множество решений уравнения х² – 5х + 6 = 0 и множество простых чисел, меньших 5.

Содержат одинаковые элементы, значит они равны (2 и 3).

Подмножества.

Определение:Если любой элемент множества В является элементом множества А, то множество В называется подмножеством (частью) множества А.

Говорят, что В содержится в А. Обозначают: В 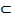А.

Или А содержит В. Обозначают: А 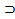В.

Например:

1. Всякое натуральное число принадлежит множеству целых чисел, т.е. N ⊂ Z или Z ⊃ N.

2. Любая точка интервала (а; в) является точкой отрезка [а; в]

3. Правильный треугольник является элементом множества всех треугольников.

В силу этого определения: любое множество является своим подмножеством А ⊂ А.

Если в множестве В найдется хотя-бы один элемент не принадлежащий множеству А, то В не является подмножеством множества А, т.е.

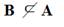
Например:

Отрезок [а; в] не является подмножеством интервала (а; в), т.к. а 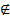(а; в) и в ∉ (а; в).

Предполагают, что 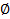является подмножеством любого множества, т.е. 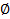⊂ А.

Таким образом:

У любого множества А всегда имеется два подмножества: А 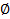⊂ А; ⊂ А.

Например:

Найти все подмножества множества А = {а; в; с}

Решение:

Подмножествами данного множества являются: {а; в; с}, {а}, {в}, {с}, {а; в}, {в; с}, {а; с}.

Операции над множествами и их свойства.