Интерполяционный многочлен в форме Лагранжа

Интерполяционный многочлен

Корень многочлена.

Все многочлены первой степени неприводимы над любым числовым полем.

Число a называется корнем многочлена, если f (a)=0.

Следствие 2.1 Многочлен степени n имеет не более n корней.

Под задачей интерполяции понимают задачу построения многочлена наименьшей степени, который в заданных точках принимает заданные значения.

Пусть требуется построить многочлен, который в точках a ₁,…, a _n (n>1) принимает значения y ₁,…, y _n. Положим w (x)=(x - a ₁)…(x - a _n) и 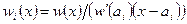. Легко убедится в справедливости равенств w _i(a _j)=0 при 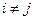и w _i(a _i)=1. Следовательно, многочлен f (x)= y ₁ w ₁(x)+…+ y _n w _n(x) принимает в точках a ₁,…, a _n значения y ₁,…, y _n.

Теорема 2.9 (Интерполяционный многочлен Лагранжа)

Существует единственный интерполяционный многочлен степени не превосходящий n- 1, который принимает в точках a ₁,…, a _n значения y ₁,…, y _n..

Доказательство. Существование доказано выше. Покажем единственность. Допустим, кроме f(x) существует ещё интерполяционный многочлен h(x) степени не выше n-1. Разность многочленов f(x)-h(x) равна 0 в точках y ₁,…, y _n., значит, по теореме Безу, она делится на w(x). Так как степень w(x) равна n, то f(x)-h(x)=0.