Разрешимые и неразрешимые свойства КС-грамматик

10.1. Разрешимые свойства КС-грамматик

Теорема. Свойство lÎL(G) разрешимо для КС-грамматик.

Разрешимость этого свойства обеспечивается алгоритмом исключения l-правил, приведенным в предыдущем разделе.

Теорема. Если G=< V_T,V_N, S, R> – КС, неукорачивающая грамматика, то язык L(G) разрешим, т.е. для любой цепочки aÎ V_T * можно определить, aÎL(G) или же aÏL(G).

Доказательство:

Пусть, aÎL(G) и½a½=n. Тогда существует вывод цепочки a I,…, b, g,…, b, …,, a. Т.е. некоторая цепочка встречается в выводе более одного раза. Тогда, удалив из вывода фрагмент g,…, b,получим опять вывод цепочки a.

Значит, для любого слова aÎL(G) существует его бесповторный вывод в G, т.е. вывод, в котором все цепочки различны, причем длина каждой цепочки £ n. Число таких цепочек ограничено числом

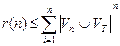, а значит, длина вывода ограничена числом r(n)!(в принципе можно дать более точную оценку, но достаточно и этой). Откуда получается простой алгоритм распознавания нам здесь aÎL(G) или же aÏL(G)?

Перебираем все бесповторные последовательности цепочек длины £ n, в которых каждая следующая цепочка не короче предшествующей, и проверяем, является ли она выводом в данной грамматике. Сложность такой проверки ограничена, т.к. на каждом шаге проверяем выводимость a_i+1 из a_i. Если хоть одна последовательность является выводом требуемой цепочки, то aÎL(G) иначе aÏL(G).

Теорема. Если G – приведенная грамматика без цепных правил, то существуют константы с1 и с2, зависящие от G, что для любого вывода D(a) цепочки aÎL(G)

c₁½a½£½D (a)½£c₂½a½, где ½D (a)½ - длина вывода цепочки a.

Доказательство:

Пусть имеется грамматика G=< V_T,V_N, S, R>.

Обозначим K - ½ V_N ½, L – максимальная длина правой части правила в R, т.е. L={max½b½/ A ®bÎR & AÎ V_N }. Т.к. G не содержит цепных и укорачивающих правил, то для любого вывода bÞ^K g, ½g½>½b½, значит, для вывода SÞ^K½a½g, ½g½>½a½, следовательно, ½D (a)½£K½a½, с другой стороны, ½a½£L½D (a)½, поэтому, ½a½/L£½D (a)½, что требовалось доказать.

Теорема.

Если G=< V_T,V_N, S, R> – КС-грамматика, то L(G) бесконечен Û существует нетерминальный символ A_i такой, что SÞ⁺ X A_i Y, A_iÞ⁺ Z A_iW, ½ZW½³ 1, и A_iÞ⁺ V&(X,Y, Z, W,VÎV_T*).

Доказательство:

Считаем, что рассматриваемая грамматика не содержит цепных правил.

1. Доказательство бесконечности языка при условии SÞ⁺ X A_i Y, A_iÞ⁺ Z A_iW, ½ZW½³ 1, и A_iÞ⁺ V очевидно, т.к. при представленных условиях фрагмент вывода A_iÞ⁺ Z A_iW может быть включен в вывод произвольное число раз; следовательно, SÞ⁺ X VY, и SÞ⁺ X Z^jVW^jY для всех j³0,что и обеспечивает построение бесконечного множества цепочек заданного вида.

2. Пусть язык, порождаемый грамматикой, является бесконечным, а условие теоремы не выполняется. Тогда максимальная глубина (длина ветви) синтаксического дерева для цепочки, порождаемой грамматикой, не превышает ½ V_N ½. Число таких деревьев конечно, значит, конечно число цепочек, порождаемых грамматикой.

Если же язык бесконечен, то глубина деревьев не ограничена, значит, в каком-нибудь синтаксическом дереве Т существует нетерминал A_i, через который ветвь дерева проходит неоднократно, причем это дерево соответствует выводу терминальной цепочки. Значит, во-первых, существует путь из начальной вешнины в данную вершину, и в силу отсутствия цепных правил, SÞ* a A_ib, aÞ*X, bÞ*Y, X,YÎV_T*, во-вторых, в силу выводимости из A_i терминальной цепочки, A_iÞ V&V_T ÎV_T, в третьих, из-за повторения нетерминала A_i в ветви дерева A_iÞ⁺dA_ie, dÞ*Z, eÞ*W, Z, W ÎV_T*, значит, A_iÞ⁺ Z A_iW, ½ZW½³ 1. Что и требовалось доказать.

Из доказанной теоремы следует

Следствие 1. Для КС-грамматики G=< V_T,V_N, S, R> существуют числа p, q такие, что для любой цепочки aÎL(G), если ½a½>p, то она имеет вид a=bgwde, где ½gd½>0, ½gwd½< q, и для любого n цепочка вида bgⁿwdⁿe ÎL(G), n³0.

Следствие 2. Язык {aⁿ bⁿ cⁿ, n³1} не порождается КС-грамматикой.

Теорема. Свойство L(G)=Æ разрешимо для КС-грамматик.

Разрешимость свойства следует из рассмотренных ранее алгоритмов: Язык L(G) не пуст тогда и только тогда, когда начальный символ грамматики является производящим.

10.2. Неразрешимые свойства КС-грамматик.

Поскольку класс множеств (слов), порождаемых грамматиками, совпадает с классом перечислимых множеств, то для языков класса «0» справедлив аналог теоремы Райса «никакое нетривиальное свойство языков класса 0 не является алгоритмически разрешимым» (Т.е. для нетривиального свойства не существует алгоритма, который по произвольной грамматике G выяснял, обладает ли данным свойством язык L(G)).

Для КЗ-грамматик проблема пустоты и бесконечности неразрешимы. Для КС-грамматик эти проблемы разрешимы.

Неразрешимые проблемы для КС-грамматик следуют из неразрешимости проблемы Поста.

Формулировка этой проблемы в виде, удобном для наших целей, следующая: для двух списков цепочек X=(a₁,a₂,…,a_m) и Y=(b₁,b₂,…b_m) в алфавите U определить, существует ли последовательность индексов i₁,i₂,…i_n, такая, что .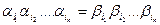

Пусть U и m фиксированы. Введём алфавит дополнительных символов U₀={b₁,b₂,…b_m}, U₀Ç U=Æ/

U₁= U₀ ÈU. Пусть X=(a₁,a₂,…,a_m) –цепочки в U. Тогда Q(X) – множество цепочек вида 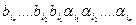, n³1.

Тогда для Q(X) справедливы утверждения

1. Если X=(a₁,a₂,…,a_m) и Y=(b₁,b₂,…b_m) списки цепочек в U, то комбинаторная проблема Поста разрешима тогда и только тогда, когда Q(X) ÇQ(Y)=Æ. Пусть существует gÎ Q(X) и gÎQ(Y). Тогда 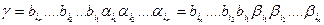, а значит,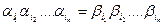

2. Для любого списка X=(a₁,a₂,…,a_m) цепочек в U, Q(X) – КС-язык в U. Соответствующая КС-грамматикаG=< V_T,V_N, S, R> для языка Q(X) - G=< U₁,{I}, I, R>; R: { I®b_i I a_i, I®b_i a_i }. Грамматика является однозначной.

Из введенных утверждений следует теорема:

Теорема. Не существует алгоритма, который по двум КС-грамматикам G₁ и G₂ определял бы, L(G₁) ÇL(G₂)=Æ?

Доказательство: Если бы такой алгоритм существовал, то проблема Поста была бы разрешима.

Теорема. Не существует алгоритма, который по любой КС- грамматике позволял бы определить, является ли эта грамматика однозначной.

Доказательство:

Рассмотрим множества Q(X) для X=(a₁,a₂,…,a_m) и Q(Y) для Y=(b₁,b₂,…b_m). Правила грамматики для порождения Q(X): R_X={ A®b_i A a_i, A®b_i a_i } правила грамматики для построения множества Q(Y): R_Y={ B®b_i B b_i, B®b_i b_i }.

Грамматика для порождения Q(X)ÈQ(Y) G=<U, {A,B}, I, R>, где R=R_XÈR_YÈ {I®A½B}. Эта грамматика однозначна, если Q(X)ÇQ(Y)=Æ, а это свойство неразрешимо.

Другие неразрешимые проблемы для КС-языков:

1. Является ли КС-языком пересечение КС-языков?

2. Является ли КС-языком дополнение КС-языков?

3. Проблема тривиальности КС-языка L=V*(= проблеме пустоты дополнения)?

4. Проблема эквивалентности КС-грамматик.