Понятие обратной позиционной кинематической задачи

Прямая позиционная кинематическая задача

Определение линейных координат точек на ЗУМ и ориентации СК ЗУМ относительно базовой СК (определение углов Эйлера) при заданных значениях координат шарниров и заданных параметрах звеньев ИМ носит название прямой позиционной кинематической задачи.

Решение прямой позиционной задачи выражается формулами

_n

t_n(0)⁽⁰⁾ = t_0n t_n(n)⁽ⁿ⁾ + S t_0j (n_j (1-s_j)q_j + l_j),

^{j =1}

где

_n

t_0n = П t_{k-1 k}

^k=1

Прямая позиционная кинематическая задача всегда имееет решение и притом единственное. Место прямой задачи в управлении МР - РИСУНОК, ИЛЛЮСТРИРУЮЩИЙ КОНТУРНОЕ УПРАВЛЕНИЕ

Определение координат сочленений по заданным линейным координатам ЗУМ и углам его ориентации относительно базовой СК при известных параметрах звеньев ИМ носит название обратной кинематической задачи о положении ИМ или обратной позиционной кинематической задачи (сокращенно, ОКЗ).

В общей постановке для многих ИМ обратная позиционная кинематическая задача может иметь несколько решений, бечсисленное множество решений или не иметь ни одного решения.

Первый случай связан с тем, что одному и тому же положению и ориентации ЗУМ относительно базовой СК может соответствовать несколько разных наборов значений координта шарниров.

Рисунок иллюстрирует один из таких случаев. Одному и тому же положению и ориентации ЗУМ изображенного на этом рисунке ИМ соответствуют 2 набора значений координат шарниров:

q1 = 0, q2 = -30 град., q3 = 0 град. (на рисунке слева)

и

q1 = 180 град, q2 = +30 град., q3 = 180 град. (на рисунке справа)

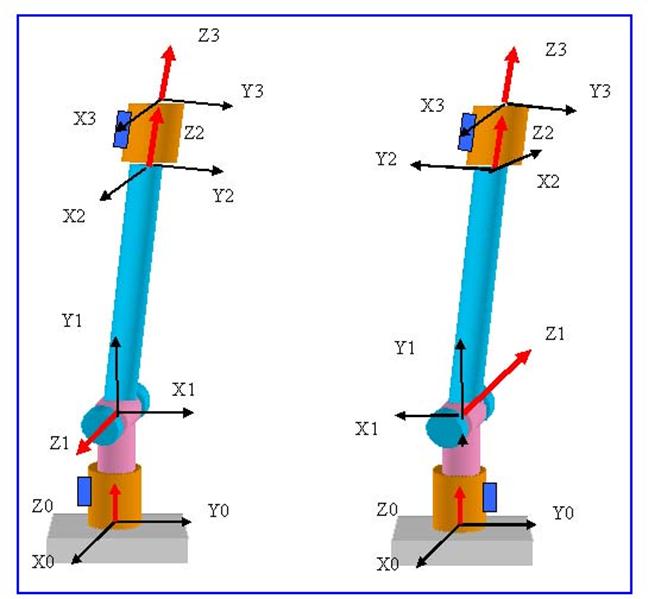
Второй случай соответствует определённым конфигурациям кинематической цепи. Для изображенногго на вышеприведенном рисунке ИМ это случай соответствует случаю, когда все звенья как бы вытянуты с линию.

Третий случай связан с ограничениями рабочей зоны вследствие конструктивных ограничений возможных значений координат сочленений и геометрических параметров звеньев ИМ.

Для обеспечения единственности решения ОКЗ применяют специальные меры.

Траектории перемещения ЗУМ предварительно планируют (ТСУ) так, чтобы исключить выход шарниров на ограничения. При этом также исключают попадание в зоны бесчисленного множества решений.

Для обеспечения единственности решения ОКЗ (в «неоднозначном» случае) в рассмотрение вводятся дополнительные параметры (индексы конфигурации кинематической цепи), позволяющие однозначно определить значения координат шарниров. Выбор этих параметров зависит от вида кинематической схемы ИМ и алгоритма решения ОКЗ.

Для изображенного на рисунке ИМ в качестве такового удобно использовать значение величины Ks, заданной нижеследующим выражением

Ks = sign (Z₁ · (Z₃ х Z₀)),

где

Z₁, Z₃, Z₀ - единичные векторы в направлении осей Z СК₁, СК₃ и СК₀, соответственно,

· - символ скалярного, а х - символ векторного произвеления векторов.

Для рассматриваемого ИМ в положении, изображенном на рисунке 1 слева Ks = 1. а в положении справа, Ks = -1.

Введение в рассмотрение индекса конфигурации Ks удобно проиллюстрировать графически. Так, в случае Ks = 1 при увеличении значения кординаты q₂ ЗУМ приближается к линии, проведенной вдоль вертикальной оси (плечо находится как бы "впереди" по ходу движения ЗУМ). В случае Ks = -1 при увеличении значения кординаты q₂ ЗУМ удаляется от вертикальной линии (плечо находится как бы "сзади" по ходу движения ЗУМ).

ПРИМЕР решения ОКЗ.

Рассмотрим 3-звенный ИМ на рис.1.

Будем считать известными углы ориентации (Pitch, Yaw, Roll) осей этой СК₃ относительно базовой СК (СК₀).

Pitch = -30 град,

Yaw = Roll = 0.

Будем считать также заданным значение индекса конфигурации Ks:

Ks = 1.

По формулам п. получим значения матрицы τ ₀₃ . В нашем случае роль СК {xyz} играет СК₀, а СК {uvw} – СК₃.

τ₀₃ = τ _{xyz, uvw} (ось u, угол Pitch) τ _{xyz, uvw} (ось v`, угол Yaw) τ _{xyz, uvw} (ось w``, угол Roll)

τ 03 = 1 0 0

0 √3/2 ½

0-1/2 √3/2

Последний столбец этой матрицы (обозначим его Z₃⁽⁰⁾) есть вектор Z₃, заданный в проекциях на оси СК₀, т.е. Z₃⁽⁰⁾.

Z₃⁽⁰⁾= (0 1/2 √3/2)^T.

Зная Z₃, вычислим вектор вектор Z₁:

Z₁ = Ks (Z₃ х Z₀)/|(Z₃ х Z₀)|.

В координатной форме последнее выражение записывается так

Z₁⁽⁰⁾ = Ks λ(Z₃⁽⁰⁾) Z₀⁽⁰⁾ /|(Z₃ х Z₀)|= - Ks λ(Z₀⁽⁰⁾) Z₃⁽⁰⁾ /|(Z₃ х Z₀)|.

где

λ(Z₃) - матрица векторного произведения, составленная из элементов вектора Z3 = (x y z)^T:

λ(Z₃) = 0 -z y

z 0 –x

-y x 0

Z₀⁽⁰⁾ = (0 0 1)^T.

Z₁⁽⁰⁾ = - (+1) 0 -1 0

1 0 0

0 0 0 (0 ½ √3/2)^T = - (- ½ 0 0)^T / (1/2) = (1 0 0)^T.

Вычислим угол q₁:

q₁ = Arctg (sin q₁ / cos q₁)

cos q₁ = X₀⁽⁰⁾ · Z₁⁽⁰⁾ = 1,

(X₀⁽⁰⁾ - единичный вектор в направлении оси X СК₀ в проекциях на оси этой же СК; X₀⁽⁰⁾ = (1 0 0)^T.

sin q₁ = Z₀⁽⁰⁾ · λ (X₀⁽⁰⁾) Z₁⁽⁰⁾ = (0 0 1) 0 0 0

0 0-1

01 0 (0 0 1)^T = (0 0 1) (0-1 0)^T = 0.

Отсюда

q₁ = 0.

Вычислим угол q₃:

q₃ = Arctg (sin q₃ / cos q₃)

cos q₃ = X₃⁽⁰⁾ · Z₁⁽⁰⁾.

X₃⁽⁰⁾ - единичный вектор в направлении оси X СК₃ в проекциях на оси СК₀; этот вектор - первый столбец матрицы τ ₀₃:

X₃⁽⁰⁾ = (1 0 0)^T.

сos q₃ = X₃⁽⁰⁾ · Z₁⁽⁰⁾ = (1 0 0) (1 0 0)^T = 1.

sin q₃ = Z₃⁽⁰⁾ · (λ (Z₁⁽⁰⁾) х X₃⁽⁰⁾) = (0 1/2 √3/2) 0 -1 0

1 0 0

0 0 0 (100)^T = 0.

Отсюда

q₃ = 0.

Вычислим угол q₂.

q₂ = Arctg (sin q₂ / cos q₂)

cos q₃ = Z₀⁽⁰⁾ · Z₃⁽⁰⁾ = (001) (0 ½ √3/2)^T = √3/2.

sin q₃ = Z₁⁽⁰⁾ · (λ (Z₀⁽⁰⁾) Z₃⁽⁰⁾) = (1 0 0) 0-1 0

1 0 0

0 0 0 (01/2√3/2)^T = (1 0 0) (-1/2 0 0)^T = -1/2.

q₂ = -30 град.

Отметим, что в общем случае решение ОКЗ требует задания помимо углов ориентации, координат точки t₃₍₀₎⁽⁰⁾ начала СК3. Однако в данном случае в силу ограниченности числа степеней свободы ИМ, достаточно задать только параметры ориентации. В данном примере решение ОКЗ можно получить, задав только линейные кординаты ЗУМ. Последовательность вычислений при этом останется прежней с той лишь разницей, что вектор Z₃⁽⁰⁾ следует вычислить как единичный вектор в направлении линии,связывающей начала 1-й и 3-й СК.