Операции над графами. Естественно стремиться представить структуру рассматриваемого графа с помощью графов меньшего размера и более простой структуры

Естественно стремиться представить структуру рассматриваемого графа с помощью графов меньшего размера и более простой структуры. Полезно дать краткие обозначения для тех графов, которые при этом часто встречаются. Уже были введены обозначения для полного графа Кр и его дополнения Кр', простого цикла Сn и простой цепи Pn, а также полного двудольного графа Km,n.

В этом разделе графы G1 и G2 имеют непересекающиеся множества вершин V1 и V2 и непересекающиеся множества ребер X1 и Х2.

Объединением G1ÈG2 таких графов называется граф множеством вершин, которого является V=V1ÈV2, а множество ребер есть X = X1ÈX2

Соединение графов, введенное Зыковым — обозначается G1+G2,состоит из G1ÈG2 и всех ребер, соединяющих V1 и V2. В частности, Кm,n = Km+Кn- Эти операции иллюстрируются на рисунке, где G1 = K2=P2 и G2=K1,2=P3

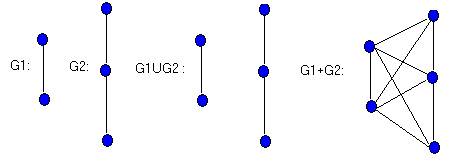
Если G — связный граф, то через nG обозначается граф с n компонентами, каждая из которых изоморфна G. Каждый граф можно записать в виде UniGi, где Gi отличается от Gj, для i! =j. Например, несвязный граф, представленный на рисунке можно записать в виде 4К1 È ЗК2 È 2K3 È К1,2

Имеется несколько операций над графами G1 и G2, которые образуют граф G с множеством вершин, равным декартову произведению Vl X V2. Среди них произведение (или декартово произведение), композиция (или лексикографическое произведение).

Чтобы определить произведение G1xG2 рассмотрим любые две вершины u=(u1, u2) и v = (v1,v2) из V = V1 X V2. Вершины u и v смежны в G1XG2 тогда и только тогда, когда [u1=v1 и u2 adj v2] или [u2=v2 и u1 adj u1]. Произведение графов G1=P2 и G2=P3 показано на рисунке

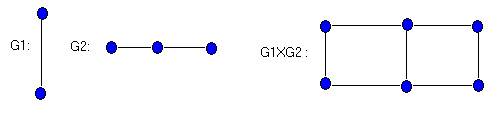
Композиция G= G1[G2] также имеет V= Vi x V2 в качестве множества вершин и вершина u=(u1,u2) смежна с v=(v1,v2) тогда и только тогда, когда [u1 asj v1] или [u1=v1 и u2 adj v2]. Для графов G1 и G2, представленных на рисунке, две композиции G1 [G2] и G2[G1], которые, очевидно, не изоморфны, показаны на рисунке

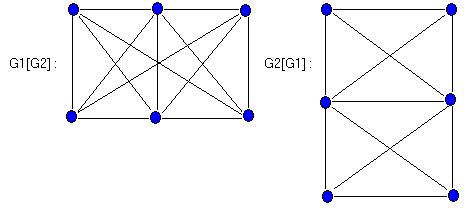
Если G1 и G2 — это (p1,q1) - и (p2,q2)-графы соответственно, то для каждой из определенных выше операций можно найти число вершин и число ребер в получающемся графе (см. таблицу 2.2).

число вершин число ребер