Точки сочленения, мосты и блоки

Точкой сочленения графа называется вершина, удаление которой увеличивает число компонент; ребро с таким же свойством называется мостом. Таким образом, если v — точка сочленения связного графа G, то граф G -v не связен. Неразделимым графом называется связный, непустой, не имеющий точек сочленения граф. Блок графа — это его максимальный неразделимый подграф. Если G — неразделимый граф, то часто он сам называется блоком.

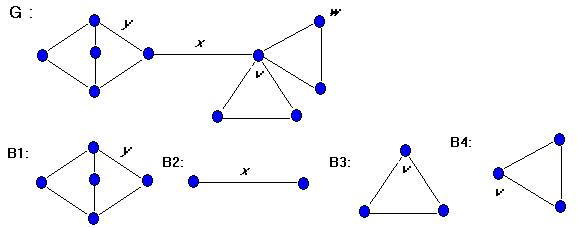
На рисунке v — точка сочленения, a w нет, х — мост, а y нет; отдельно приведены четыре блока графа G. Каждое ребро графа принадлежит точно одному из его блоков, так же как и каждая вершина, не являющаяся ни изолированной, ни точкой сочленения. Далее, ребра любого простого цикла графа G также принадлежат только одному блоку. Отсюда, в частности, следует, что блоки графа разбивают его ребра и простые циклы на множества, которые можно рассматривать как множества ребер. В первых трех теоремах этой главы устанавливаются несколько эквивалентных, условий, обеспечивающих существование у графа точки сочленения и моста и неразделимость графа.

Теорема. Пусть v — вершина связного графа G. Следующие утверждения эквивалентны:

(1) v — точка сочленения графа G;

(2) существуют такие вершины u и w, отличные от v, что v принадлежит любой простой (u-w)-цепи;

(3) существует разбиение множества вершин V— {u} на такие два подмножества U и W, что для любых вершин u Î U и w Î W вершина v принадлежит любой простой (u-w)-цепи.

Доказательство. (1) влечет (3). Так как v — точка сочленения графа G, то граф G - y не связен и имеет по крайней мере две компоненты. Образуем разбиение V—{u}, отнеся к U вершины одной из этих компонент, а к W — вершины всех остальных компонент. Тогда любые две вершины u Î U и w Î W лежат в разных компонентах графа G—v. Следовательно, любая простая (u-w)-цепь графа G содержит v.

(3) влечет (2). Это немедленно следует из того, что (2) — частный случай утверждения (3).

(2) влечет (1). Если v принадлежит любой простой цепи в G, соединяющей u и w, то в G нет простой цепи, соединяющей эти вершины в G -v. Поскольку G - u не связен, то u -точка сочленения графа G.

Теорема. Пусть х — ребро связного графа G. Следующие утверждения эквивалентны:

(1) х — мост графа G;

(2) х не принадлежит ни одному простому циклу графа G;

(3) в G существуют такие вершины u и v, что ребро х принадлежит любой простой цепи, соединяющей u и v;

(4) существует разбиение множества V на такие подмножества U и W, что для любых вершин u Î U и w Î W ребро х принадлежит любой простой (u-w)-цепи.

Теорема. Пусть G — связный граф с не менее чем тремя вершинами. Следующие утверждения эквивалентны:

(1)G — блок;

(2) любые две вершины графа G принадлежат некоторому общему простому циклу;

(3) любая вершина и любое ребро графа G принадлежат некоторому общему простому циклу;

(4) любые два ребра графа G принадлежат некоторому общему простому циклу;

(5) для любых двух вершин и любого ребра графа G существует простая цепь, соединяющая эти вершины и включающая данное ребро;

(6) для любых трех различных вершин графа G существует простая цепь, соединяющая две из них и проходящая через третью;

(7) для каждых трех различных вершин графа G существует простая цепь, соединяющая две из них и не проходящая через третью.

Доказательство. (1) влечет (2). Пусть u, v - различные вершины графа G, и U - множество вершин, отличных от u, которые лежат на простом цикле, содержащем u. Поскольку в G, по крайней мере три вершины и нет точек сочленения, то в G нет также мостов. Значит, каждая вершина, смежная с u, принадлежит U, т. е. U не пусто.

Предположим, что v не принадлежит U. Пусть w - вершина в U, для которой расстояние d(w, v) минимально. Пусть Р0 — кратчайшая простая (u-w)-цепь, и P1 и Р2 - две простые (u-v)-цепи цикла, содержащего u и w (смотри рисунок). Так как w не является точкой сочленения, то существует простая (u-v)-цепь Р', не содержащая w. Обозначим через w' ближайшую к u вершину, принадлежащую Р', которая также принадлежит Р0, и через u' последнюю вершину (u-w')-подцепи в Р', которая принадлежит или P1 или Р2. Не теряя общности, предположим, что и' принадлежит P1.

Пусть Q1 -простая (u-w')-цепь, содержащая (u-u')-подцепь цепи P1 и (u-w')-подцепь цепи Р', и Q2 - простая (u-w')-подцепь, содержащая Р2 вслед за (w - w') - подцепью цепи Р0. Ясно, что Q1 и Q2 - непересекающиеся простые (u-w')-цепи. Вместе они образуют простой цикл, так что u' принадлежит U. Поскольку w' принадлежит кратчайшей цепи, d(w', v)<d(w, v). Это противоречит выбору w и, следовательно, доказывает, что u uv лежат на одном простом цикле.

(2) влечет (3). Пусть u - вершина, vw -ребро графа G, и Z — простой цикл, содержащий u и vw. Простой цикл Z', содержащий u и vw, можно образовать следующим образом. Если w лежит на Z, то Z' содержит vw и (w-u)-подцепь в Z, содержащую u. Если w не лежит на Z, то существует (w-u)-цепь Р, не содержащая v, поскольку иначе по теореме v — точка сочленения. Пусть u -первая вершина цепи Р в Z. Тогда Z' содержит vw вслед за (w-u')-подцепью цепи Р и (u-v')-цепью в Z, включающей u.

(3) влечет (4). Доказательство, как в предыдущем случае.

(4) влечет (5). Каждая из двух вершин графа G инцидентна некоторому ребру; соответствующие ребра в силу утверждения (4) лежат на одном простом цикле. Следовательно, любые две вершины графа G принадлежат одному простому циклу, а отсюда следует (2) и, значит, (3). Пусть u, w, v — различные вершины, х - ребро графа G. Из утверждения (3) получаем, что существуют простой цикл Z2, содержащий u и х, и простой цикл Z2, содержащий v и х. Таким образом, нужно рассмотреть только случай, когда v не лежит на Z1, а u не лежит на Z2. Начнем идти из u по Z1 до тех пор, пока не достигнем первой вершины w цикла Z2, затем пойдем по цепи на Z2, которая соединяет w и v и содержит х. Такой обход образует простую цепь, соединяющую u и v и содержащую х.

(5) влечет (6). Пусть u, v и w - различные вершины графа G, и х - произвольное ребро, инцидентное w. Из утверждения (5) вытекает, что существует простая цепь, соединяющая u и v, которая содержит x и, следовательно, должна содержать w.

(6) влечет (7). Пусть u, v и w - различные вершины графа G. Из утверждения (6) вытекает, что существует простая (u-w)-цепь Р, содержащая v. Ясно, что (u-v)-подцепь цепи Р не содержит w.

(7) влечет (1). Используя (7), получаем, что для любых двух вершин u и w ни одна из остальных вершин не может принадлежать каждой (u-w)-цепи. Следовательно, G должен быть блоком.

Теорема. В любом нетривиальном связном графе найдутся по крайней мере две вершины, не являющиеся точками сочленения.

Доказательство. Пусть u и v — вершины графа G, максимально удаленные друг от друга, т. е. такие, что d(u, v)=d(G). Предположим, что v -точка сочленения. Тогда существует вершина w, принадлежащая той компоненте графа G - v, которая не содержит вершину u. Значит, v лежит на любой цепи, соединяющей w и u, и поэтому d(u, w)>d(u, v), что невозможно. Следовательно, v, а также u не являются точками сочленения графа G.