Некоторые свойства реберных графов

Реберные графы

Понятие реберного графа для данного графа настолько естественно, что независимо было введено многими авторами. Конечно, каждый из них давал свое название: Ope назвал этот граф «смежностным графом», Сабидусси - «графом производной», Байнеке — «производным графом», Сешу и Рид - «реберно-вершинно-двойственным», Кастелейн — «покрывающим графом», Менон - «присоединенным» («сопряженным»). Были даны различные описания реберных графов. В этой главе вводится также тотальный граф, который изучался впервые Бехзадом, и поскольку (это очень удивительно!) он был обнаружен единожды, он не имеет других названий. Мы исследуем связь между реберными и тотальными графами, уделяя особое внимание эйлеровым и гамильтоновым графам.

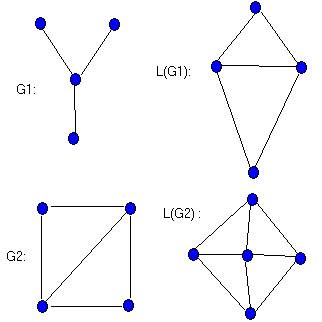
Рассмотрим множество X всех ребер графа G как семейство двухвершинных подмножеств множества V(G). Реберным графом графа G - обозначается L(G)- называется граф пересечений W(X). Таким образом, вершинами графа L (G) являются ребра графа G и две вершины графа L (G) смежны тогда и только тогда, когда смежны соответствующие им ребра графа G. Если x = uv - ребро графа G, то ясно, что степень вершины x в графе L (G) равна degu + degw - 2. Два примера графов и их реберных графов приведены на рис. Заметим, что на этом рисунке G2=L(G1), так что L(G2) = L (L (G1)). Запишем L1 (G)=L (G),

L2 (G)=L (L (G)) и в общем случае определим итерированный реберный граф рекуррентным соотношением Lⁿ(G)=L(L^n-1(G)), n>2.

Непосредственно из определения графа L (G) вытекает, что каждая точка сочленения графа L (G) есть мост графа G, не являющийся концевым ребром, и обратно.

Если определен некоторый класс графов, то полезно знать оценку числа вершин и ребер в каждом графе данного класса. Это легко сделать для реберных графов.

Теорема. Если G - это (р,q)-граф с вершинами, имеющими степени di, то L (G) имеет q вершин и qL ребер, где

qL=-q+1/2Edf.

Доказательство. По определению реберного графа граф L (G) имеет q вершин. Каждые di ребер, инцидентных вершине vi дают вклад (di,2) в число ребер графа L(G), так что

qL = E(di,2) = 1/2Edi(di-1) = 1/2Edi*di - 1/2Edi = 1/2Edi*di - q

Следующий результат вы можете установить многими разными способами в зависимости от вашего желания.

Теорема. Связный граф G изоморфен своему реберному графу L (G) тогда и только тогда, когда G - простой цикл.

Таким образом, для графа G (не обязательно связного) G=L(G) тогда и только тогда, когда G — регулярный граф степени 2.

Если графы G1 и G2 изоморфны, то, очевидно, что графы L(G1) и L(G2) также изоморфны. Уитни установил, что обратное справедливо почти всегда, и указал при этом единственную пару различных графов, имеющих один и тот же реберный граф. Доказательство, данное здесь, принадлежит Юнгу.

Теорема. Пусть G и G'— связные графы, у которых реберные графы изоморфны. Графы G и G' изоморфны всегда, кроме случая, когда один из них есть Кз, а другой K₁,з

Доказательство. Заметим сначала, что среди связных графов с не более чем четырьмя вершинами единственной парой различных графов с изоморфными реберными графами являются Кз и К_1,3, Кроме того, нетрудно видеть, что изоморфизм F графа G на граф G' индуцирует изоморфизм F1 графа L(G) на граф L(G'). Докажем более сильный результат, из которого будет следовать наша теорема.

Если в графах G и G' более четырех вершин, то любой изоморфизм F1 графа L (G) на граф L (G) индуцируется точно одним изоморфизмом графа G на граф G'.

Прежде всего, докажем, что F1 индуцируется не более чем одним изоморфизмом. Предположим противное, т. е. что имеются два таких изоморфизма, скажем F и Y, и покажем, что F (v)= Y (v) для любой вершины v графа G. В самом деле, в графе G существуют два ребра x=uv и y=vw или два ребраx=uv и y=uw. Если y=vw, то обе вершины F (v) и Y (v) принадлежат каждому из ребер F (x) и F (y). Но поскольку у этих ребер только одна общая вершина, то F (w) =Y (u). Аналогично рассматривается случай v=uw: так как ребро F1(х) содержит две вершины F (v) иF (u)= Y (u), то опять имеем F(v)= Y (u). Следовательно, F1 индуцируется самое большее одним изоморфизмом графа G на граф G'.

Докажем теперь существование изоморфизма F, индуцирующего F. Сначала покажем, что ребра x1 =uv1, x2=uv2 и x3=uv3 подграфа K_l,3 графа G должны переходить при отображении F в ребра подграфа К_1,3 графа G'. Пусть у — другое ребро, смежное по крайней мере с одним из ребер xi и такое, что оно смежно или с одним, или сразу с тремя ребрами xi. Такое ребро y существует в любом графе с р> 5 вершинами, а для P<5 теорема тривиальна. Если три ребра F1(х) образуют не К_1,3, а треугольник, то ребро F1 (у) должно быть смежно точно с двумя из них. Следовательно, любой подграф К_1,3 должен переходить в К_1,3.

Обозначим через S (v) множество ребер, инцидентных v. Покажем, что для каждой вершины v графа G существует точно одна такая вершина v' графа G', что S (v) при отображении F, переходит в S (v'). Если deg v> 2, обозначим через у1 и y2 ребра, инцидентные v, и пусть и' — общая вершина ребер (F1(y1) и F2(y2) Тогда для каждого ребра х, инцидентного v, вершина v' инцидентна (Ф1(x), и для каждого ребра х', инцидентного v', вершина v инцидентна Ф1(х) Если deg v = 1, то пусть x=uv - ребро, инцидентное v. Тогда deg «^ ^2, и, следовательно, множество S (u) переходит в множество S(u') и (F1(x) = u'v'. Поскольку для каждого ребра х', инцидентного v', ребра Fl(x') и х должны иметь общую вершину, то вершина u принадлежит ребру Ф1l(x'), а вершина u' - ребру х', т.е. х' = F1(x) и deg v' = l. Итак, S(u)=S(v) только тогда, когда u=v. Следовательно, отображение F множества V в множество V взаимно однозначно.

Далее, для данной вершины v' из V существует инцидентное ей ребро х'. Обозначим Ф1'(х') через uv. Тогда или F (u)=u', или F(v) = v', так что F - отображение «на».

Наконец, заметим, что F1(x)= F (u) F (v) для каждого ребра x - uv графа G и

Ф11 (х')= F11(u') F11(v') для каждого ребра х' = = u'v' графа G', так что F - изоморфизм, индуцирующий изоморфизм Ф1. Теорема доказана.