Хроматический многочлен

Хроматический многочлен графа введен Биркгофом и Льюисом, когда они предпринимали попытки решить гипотезу четырех красок. Пусть G - помеченный граф. Раскраской графа G t цветами называется раскраска графа G, использующая t или меньше цветов. Две раскраски графа G t цветами будем считать различными, если, по крайней мере, одной помеченной вершине приписываются различные цвета.

Обозначим через f(G,t) число различных раскрасок помеченного графа G

t цветами. Если t<хr(G), то естественно, f(G, t)=0. Наименьшее из чисел t, для которых f(G,t) > 0, есть, очевидно, хроматическое число графа G. Следовательно, в гипотезе четырех красок утверждается, что f(G, 4)> 0 для каждого планарного графа G.

Например, любую данную вершину полного графа Кз можно окрасить t способами. Для второй вершины можно взять любой из t—1 цветов, и, наконец, третья вершина окрашивается t—2 способами. В результате

f(Kз, t) = t(t-1) (t-2)

Эту формулу можно обобщить на любой полный граф:

f(KP, t) = t(t-1) (t-2)... (t-p + l)=(f)p

Особенно легко найти соответствующий многочлен для вполне несвязного графа Кр, так как каждую из его р вершин можно окрасить независимо t способами:

f(K_p,t) = t^p

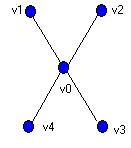
Центральную вершину v0 графа К1,4 показанного на рисунке, можно окрасить t способами, а любую из висячих вершин t—1 способами. Поэтому

f(К_1,4, t)=t(t-1)⁴

Во всех приведенных примерах f(G,t) есть многочлен от переменной t. Это всегда так, в чем мы сейчас убедимся.

Теорема. Если u и v — несмежные вершины графа G, а e — элементарный гомоморфизм, отождествляющий их, то

f(G, t)=f(G+uv,t)+f(eG, t)

Доказательство. Это равенство следует непосредственно из двух замечаний. Первое - число способов раскраски графа G t цветами, когда вершины и и v окрашиваются в разные цвета, равно числу способов раскраски графа G+uv t цветами. Второе - число способов раскраски графа Gt цветами, когда вершины u и v окрашиваются в один цвет, равно числу способов раскраски гомоморфного образа eG t цветами, где e отождествляет u и v.

Следствие (a). f(G,t) — многочлен от переменной t для любого графа G.

Назовем f(G, t) хроматическим многочленом графа G. Для иллюстрации теоремы воспользуемся приемом, предложенным Зыковым. В соответствии с этим приемом хроматический многочлен графа,

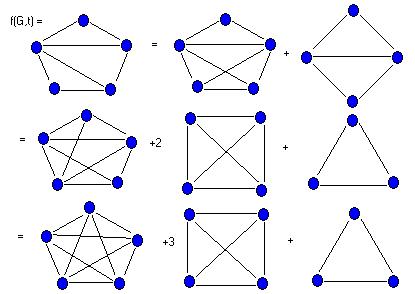
зависящий от t, обозначается с помощью диаграммы графа. На каждом шаге этого процесса выбираем две несмежные вершины и, v и дальше представляем граф так, как предлагает Рид.

Так, для графа G, показанного на рис. 12.15, получаем многочлен

f(G,t) = (t)5+3(t)4+(t)3 = t⁵-7t⁴+18t³-20t²+8t.

В частности, граф G можно раскрасить тремя цветами f(G, 3)=6 способами.

Перечислим некоторые свойства хроматических многочленов, вытекающие непосредственно из теоремы.

Теорема. Пусть G — граф с р вершинами, q ребрами и k компонентами

G1,G2,..., Gk. Тогда

1) f(G, t) имеет степень р;

2) коэффициент при tp в f(G, t) равен 1;

3) коэффициент при t p-1 в f(G, t) равен - q;

4) свободный член многочлена f(G, t) равен 0;

5) наименьший показатель у степеней переменной t, входящих в f(G, t) с ненулевыми коэффициентами, есть k.

Совсем не очевиден следующий результат, полученный Уитни и обобщенный Рота, использовавшим свои мощные методы, в которых привлекается обратное преобразование Мёбиуса.

Теорема. Коэффициенты любого хроматического многочлена меняются по знаку.

Ясно, что каждые два изоморфных графа имеют один и тот же хроматический многочлен. Однако часто несколько неизоморфных графов также имеют один и тот же хроматический многочлен. Например, у всех деревьев с р вершинами один хроматический многочлен.

Теорема. Граф G с р вершинами является деревом тогда и только тогда, когда

f(G, t) = t(t-1)p-1

Остается нерешенной задача описания графов, имеющих один и тот же хроматический многочлен. Более общая нерешенная задача состоит в нахождении необходимого и достаточного условия для того, чтобы многочлен был хроматическим. Например, многочлен t4 -3t3+3t2 обладает всеми известными свойствами хроматического многочлена, но не является хроматическим. Если бы существовал граф G с таким хроматическим многочленом, то он должен был бы иметь 4 вершины, 3 ребра и 2 компоненты, так что G=K3 È K1. Однако хроматический многочлен последнего графа равен

f(G,t) = (t)3* t = t4 -3t3+3t2

Рид предположил, что абсолютные значения коэффициентов любого хроматического многочлена сначала строго возрастают, затем строго убывают и, наконец, не меняются.