2014-02-02
248
Если сущ. lim (an+1)/an=D, то при D<1 ряд (1) сх-ся при D>1- расх-ся, причём lim an=+¥
1 Если lim (an+1)/an<1, то ($ q>0):[ lim (an+1)/an<q<1]. По сл-ию о сохр. нер-ва Т-6.5. нач. с нек. номера n будет (an+1)/an<q. Благод. 1.5. мож. Счит., что ("n)[ (an+1)/an < q],знач.("n)[an+1<an×q]Þa2<a1×q,a3<a2×q<(a1×q)×q=a1×q2Þa3<a1×q2Þ…an<a1×qn-1. Т.к. геом. р. Sa1×qn-1 при 0<1 сх-ся, то по пр-ку срав. Сх-ся ряд San. Пусть lim (an+1)/an>1, тогда ($q):[ lim (an+1)/an>q>1]. При дост. больших номрах n будет (an+1)/an>qÛan+1>an×q, мож. счит., что это верно при всех ном-х n, отсюда ан-но предыдущему получаем an>a1×qn-1; но lim a1×qn-1=+¥Þ lim an=+¥, ряд расх-ся.g
10.Теор Радикальный признак Коши.
Если $ lim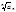 
=c, то при с<1 ряд сх-ся, при c>1- расх-ся, причём lim an=+¥
1Самост. Ан-но теореме 2.4. Исп-ть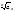 
><qÞan><qng
11.Теор Инт-й признак Коши.
Если члены ряда San являются знач-ми некот. неотр. убывающей ф-ии f(x), непрерывной на [1,+¥[: a1=f(1),a2=f(2),…,an=f(n),…, то ряд сх. Или расх. одноврем. с несоб. инт-ом ò(1 to +¥)f(x)dx.
Сумма San выраж. Площадь ступ. фигуры с беск. Основанием [0, +¥[, а ò(1 to +¥)f(x)dx – пл-дь криволю трапеции с бескон основанием [1, +¥[ под графиком y=f(x). Утв-ся, что обе эти площади конеч. или бескон. одновременно.
1 Согл. критерию сх-ти несоб. инт-ла от неотр. ф-ии инт-л сх-сяÛ Ф(х)= ò(1 to x)f(t)dt ограничена на [1, +¥[, а согл. кр-ю сх-ти +го ряда, ряд San сх-ся Û посл-ть частич. Сумм {Sn} огр-на. Ввиду убывания f k<x<k+1Þf(k)³f(x)³f(x+1)Þak³f(x)³a k+1 Þ ò(k to k+1)ak×dx³ò(k to k+1)f(x)dx³ò(k to k+1)a k+1dxÞak³ò(k to k+1)f(x)dx³a k+1 ÞS(k=1 to n)ak³S(k=1 to n) ò(k to k+1)f(x)dx³S(k=1 to n)a k+1 Þ Sn³ò(1 to n+1)f(x)dx³Sn+1-a1ÞSn³Ф(n+1)³Sn+1-a1.
Если ò(1 to +¥) сх-ся, то {Ф(n+1)} ограничена, тогда из нер-ва Sn+1£ Ф(n+1)+a1Þ что { Sn+1}
Ограничена и потому San сх-ся. Если же ò(1 to +¥) расх-ся, то {Ф(n+1)} неограничена, а из нер-ва Sn³Ф(n+1)Þ {Sn} неограничена и потому ряд расх-сяg
12.Пример
S(1/na) – наз-ся общим гармоническим рядом (Дирихле), сх-ся при a>1 и расх. при a£1.
1 ò(1 to +¥)dx/xa - сх-ся при a>1 и расх. при a£1. При a>0 ф-я f(x)=1/xa будет убывающей, неотрицательной, непрерывной на [1, +¥[, причём f(n)= 1/na=an. Поэт. Согл. 2.6. данный ряд сх-ся или расх. одноврем. с интегралом.
При a<0 an=1/na ® +¥, а пр a=0 an=1®1 an не ®0 Þ ряд расх-ся. Т.о. при всех -¥<a£1 ряд расх., при a>1 сх-ся.g
14.Теор Об абсолютной сходимости.
Если сходится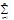 
|an|, то сх-ся и сам 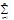an.
1 [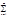
|an|-сх-ся ]Þ(*крит Коши*)Þ("e>0)($ n e):("m>n>ne)[|
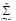|an||<eÞ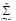|an|<e].Но 
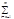|an||£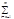|an|Þ("e>0)($ne):("m>n>ne)[|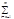an|]<e]Þ(*крит. Коши*)Þ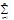an сх-ся.g
