Лекция 14 5 страница

Используя зависимость между передаточными функциями замкнутой Ф(р) и разомкнутой W(p) системы, можно записать

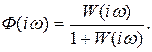(5.18)

Выделяя действительные и мнимые части функций Ф(р) и W(р), получим

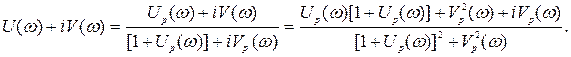
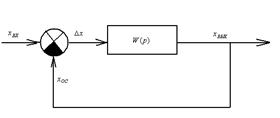
Рис. 5.3

Таким образом

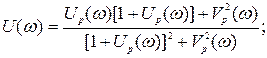(5.19)

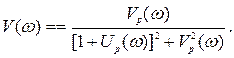(5.20)

Выражение (5.19) связывает вещественную частотную характеристику замкнутой системы U(ω) с вещественной U_р(ω) и мнимой V_р(ω) частями АФЧХ разомкнутой системы.

По формуле (5.19) построена номограмма (вещественная частотная диаграмма), которая позволяет определять ординаты вещественной частотной характеристики замкнутой системы по АФЧХ разомкнутой системы (рис. 5.4).

Номограмма представляет собой линии равных значений вещественной частотной характеристики, построенные в плоскости АФЧХ W(iω)=U_р(ω)+iV_р(ω) разомкнутой системы.

Если при исследовании устойчивости использовались ЛАФЧХ, то для построения, вещественной характеристики можно воспользоваться аналогичными номограммами, приведенными в литературе.

5.4. ПОСТРОЕНИЕ АФЧХ ЗАМКНУТОЙ СИСТЕМЫ ПО ЧАСТОТНЫМ ХАРАКТЕРИСТИКАМ РАЗОМКНУТОЙ СИСТЕМЫ. ИСПОЛЬЗВАНИЕ АФЧХ ЗАМКНУТОЙ СИСТЕМЫ ДЛЯ ИССЛЕДОВАНИЯ ВЫНУЖДЕННЫХ КОЛЕБАНИЙ И ПОСТРОЕНИЯ ВЕЩЕСТВЕННОЙ ХАРАКТЕРИСТИКИ.

При исследовании устойчивости САУ пользуются ЛЧХ разомкнутой системы. Расчет установившихся ошибок или исследование вынужденных колебаний при гармонических воздействиях производят с помощью ЛЧХ замкнутой системы. ЛЧХ замкнутой системы можно использовать также для построения вещественной частотной характеристики, по которой строится кривая переходного процесса. Это приводит к необходимости перехода от ЛАХ и ФЧХ разомкнутой системы к соответствующим характеристикам замкнутой системы.

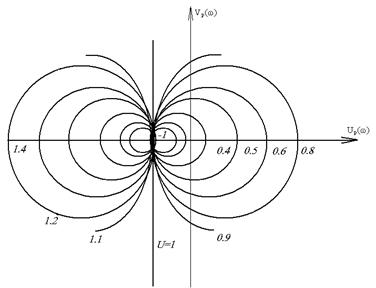
Рис. 5.4

Для этой цели можно воспользоваться номограммой замыкания, которая построена для единичной обратной связи (рис. 5.3).

Если система или местный замкнутый контур имеют неединичную обратную связь, то их структурные схемы необходимо преобразовать к виду, показанному на рис. 5.5.

В основу построения номограммы для замыкания системы положена формула (5.18).

АФЧХ замкнутой и разомкнутой системы можно представить в следующем виде:

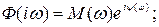(5.21)
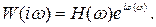(5.22)

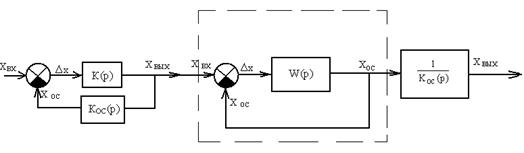
Рис. 5.5

Подставляя формулы (5.21) и (5.22) в выражение (5.18), получим

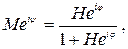
или 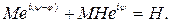(5.23)

Разложив 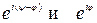по формуле Эйлера, выражение (5.23) перепишем в виде

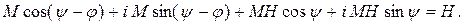
Приравнивая мнимые и действительные части полученного выражения, можно записать:

М соs (ψ – φ)+МН соs ψ =Н; (5.24)
sin (ψ – φ)+H sin ψ = 0. (5.25)

Уравнения (5.24) и (5.25), предварительно записанные в логарифмическом масштабе, позволяют построить в плоскости Н_дБ , φ° линии равных значений М_дБ и ψ°. Совокупность линий М_дБ и ψ°, построенных в плоскости Н_дБ , φ° называется номограммой замыкания системы (рис.5.6).

Чтобы найти ординаты логарифмической амплитудной М_дб и фазовой ψ° характеристик функции Ф(iω) при некотором фиксированном значении частоты ω ₁, надо для разомкнутой системы определить значения Н(ω₁)_дБ и φ°(ω₁) и отложить их по осям номограммы.

Проводя через точки Н(ω₁)_дБ и φ°(ω₁) соответственно горизонталь и вертикаль, получим точку их пересечения в плоскости номограммы. Кривые М_дБ и ψ°, проходящие через эту точку, равны соответственно значениям ординат ЛАЧХ и ЛФЧХ замкнутой системы при частоте ω ₁. Аналогично определяются М_дБ и ψ° при других фиксированных значениях частоты и получаются таким образом зависимости М_дБ (ω) и ψ°(ω). Процесс замыкания можно существенно упростить, если воспользоваться следующими рекомендациями.

При Н >>1 в выражении 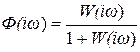единицей в знаменателе можно пренебречь, тогда Ф(iω) ≈ 1, т.е.

М_дБ ≈ 0 и ψ° ≈ 0.

Учитывая это, приходим к выводу, что продолжать номограмму вверх за значения Н_дБ =25 ÷ 30 дБ не имеет смысла, т.к. для значений Н_дБ > 25 дБ можно считать, что М_дБ = 0 и ψ° = 0.

При H<<1 будем иметь Ф(iω) ≈ W(iω), т.е. при больших по абсолютному значению отрицательных Н_дБ частотные характеристики разомкнутой и замкнутой систем совпадают, поэтому продолжать номограмму вниз за значение - (25÷30) дБ также не имеет смысла, т.к. для значений Н_дБ < – 25 дБ М_дБ ≈Н_дБ , а ψ° ≈ φ°.

Представленные на номограмме кривые симметричны относительно вертикальной оси, проходящей через точку с координатой φ°= – 180°, причем индексы симметричных половин кривых М_дБ совпадают как по величине, так и по знаку, а индексы симметричных кривых ψ°, будучи одинаковыми по величине, различаются знаком (например, кривой с индексом ψ° = – 60° соответствует в левой половине номограммы симметричная кривая с индексом ψ° = 60° = – 300°). В силу этой симметрии полную номограмму можно заменить ее половиной, соответствующей значениям φ° от 0 до –180 °. Для удобства некоторые номограммы снабжены шкалой φ° с двойной индексацией.

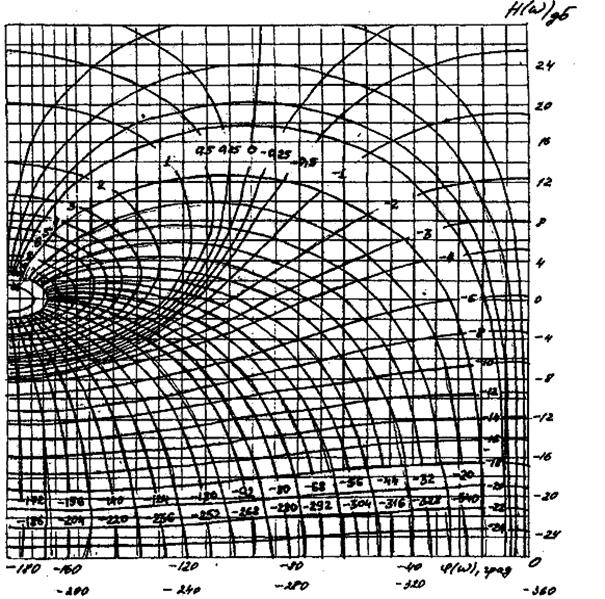
Рис.5.6

Номограмма может быть применена для построения характеристик передаточной функции по ошибке

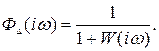
Для этого достаточно иметь в виду следующую зависимость:

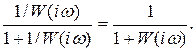
Действительная часть АФЧХ замкнутой системы (вещественная частотная характеристика) U(ω) связана с модулем (АЧХ) М(ω) и аргументом (ФЧХ) ψ°(ω) замкнутой системы следующим выражением:

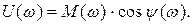(5.26)

Таким образом, имея ЛАФЧХ замкнутой системы, можно легко построить вещественную характеристику. Для этого достаточно перейти от логарифмического масштаба М_дБ (ω)=20lgМ(ω) к обычному М(ω) и воспользоваться формулой (5.26).

Характеристику М(ω) используют для анализа вынужденных колебаний САУ при гармоническом внешнем воздействии.

В самом деле, АЧХ замкнутой системы

,

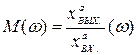т.е. 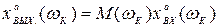, (5.27)

где 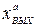- амплитуда выходной величины;

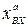- амплитуда входной величины;

ω_к - фиксированное значение частоты воздействия.

Таким образом, если 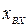= 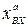sin ωt, то 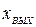= 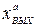sin (ωt+ ψ°), где 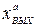определяется по выражению (5.27), а ψ° – по ФЧХ замкнутой системы.

ЛЕКЦИЯ 15

План лекции:

1. Оценки качества, связанные с распределением нулей и полюсов

передаточной функции.

2. Степень устойчивости и колебательность САУ.

3. Диаграмма качества.

4. Рекомендуемая литература [7, 1, 6 ].

5.5. КОСВЕННЫЕ ОЦЕНКИ КАЧЕСТВА, СВЯЗАННЫЕ С РАСПРЕДЕЛЕНИЕМ НУЛЕЙ И ПОЛЮСОВ ПЕРЕДАТОЧНОЙ ФУНКЦИИ

Косвенные оценки качества позволяют определить основные показатели качества без построения кривой переходного процесса, т.е. косвенными методами. Являясь приближенными оценками, они позволяют существенно сократить время исследования САУ.

В общем случае дифференциальное уравнение линейной САУ имеет вид

.

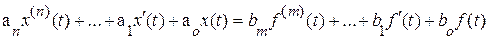Изображение Х (р) можно записать в виде

,

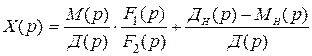или

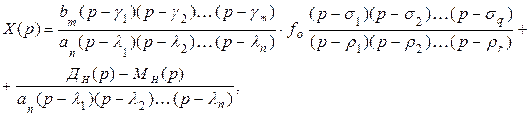(5.28)

где l1,l2,...,ln – корни характеристического уравнения Д(р) называются полюсами передаточной функции;

g1,g2,...,gm – корни уравнения М(р) - нули передаточной функции;

s1,s2,...,sq – корни уравнения F1(p)=0 - нули воздействия;

r1,r2,...,rr – корни уравнения F2(p)=0 - полюсы воздействия.

Выражение (5.28) показывает, что в общем случае движение системы в переходном режиме зависит от нулей и полюсов передаточной функции, нулей и полюсов воздействия, начальных условий по всем переменным.

Переходя к оригиналу, в соответствии со второй теоремой разложения будем иметь

x(t)=xc(t)+xв(t),

где xc(t)=xcc(t)+xcд(t):

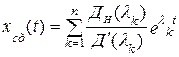; (5.29)

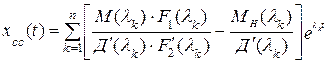; (5.30)

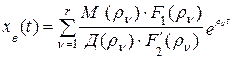. (5.31)

Анализ выражений позволяет сделать следующие выводы:

1. Свободное движение хсд(t), вызванное начальным состоянием системы, не зависит от нулей и полюсов воздействия и полностью определяется корнями характеристического уравнения и начальными условиями переменной х(t) и ее производных. Чем дальше расположены полюсы передаточной функции от мнимой оси на плоскости комплексного переменного р, тем быстрее затухают свободные колебания.

2. Составляющая собственного движения хсс(t) зависит oт относительного расположения нулей и полюсов передаточной функции

М(lк)= bm(lк-g1)(lк-g2)¼(lк-gm), (5.32)

от относительного расположения полюсов передаточной функции и нулей воздействия

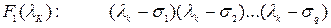(5.33)

и от относительного расположения полюсов передаточной функции и полюсов воздействия.

.

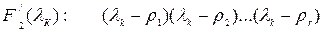Выражения (5.32) и (5.33) позволяют так выбрать соотношение нулей и полюсов передаточной функции и воздействия, чтобы амплитуда собственных колебаний была бы минимальна.

Так, чем ближе нули воздействия к полюсам передаточной функции и чем дальше расположены полюсы воздействия от полюсов передаточной функции, тем меньше величина первого слагаемого в выражении (5.30).

Так же целенаправленно можно уменьшать и второе слагаемое в этом выражении.

3. Вынужденное движение хв(t) зависит от относительного расположения полюсов воздействия и нулей передаточной функции

М(r_n)= bm (rn-g1)(rn-g2)¼(rn-gm), (5.34)

от взаимного расположения нулей и полюсов воздействия

F1(rn) = f₀ (rn-s1)(rn-s2)¼(rn-sq)

и от относительного расположения полюсов воздействия и полюсов передаточной функции

Д(rn) = an (rn-l1)(rn-l2)¼(rn-ln).

Если f(t) представляет собой возмущающее воздействие, то вынужденные колебания, вызванные этим воздействием, необходимо исключить или хотя бы уменьшить амплитуду этих колебаний. Для этого нули передаточной функции и нули воздействия должны располагаться на плоскости р как можно ближе к полюсам воздействия, а полюсы передаточной функции должны находиться как можно дальше от полюсов воздействия.

Если f(t) представляет собой управляющее воздействие, то система должна воспроизводить его, как можно точнее, т.е.

xв(t)» f(t). В этом случае при выборе структуры и параметров САУ необходимо стремиться к тому, чтобы М(rn)»Д(rn) Решение поставленной задачи в общем виде для систем высокого порядка связано с большими трудностями, поэтому на практике ограничиваются рассмотрением частных случаев.

Полагают, например, что начальные условия по всем переменным

нулевые, т.е. ДН(р)=0 и МН(р), внешнее воздействие принимается в виде f(t)=c× 1 (t), т.е. 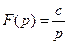, считают, что многочлен М(р) не зависит от р. В этом случае уравнение (5.28) принимает вид

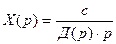
и движение системы в переходном режиме полностью определяется полюсами передаточной функции, т.е. корнями уравнения

Д(р) = 0.

Таким образом, о качестве регулирования можно судить по расположению полюсов передаточной функции λ₁, λ₂,…, λ_n на плоскости комплексного переменного р=d ± iw.

О характере расположения полюсов передаточной функции на плоскости р судят, по координатам трапеции (рис.5.7), внутри которой расположены все корни lk, а ближайшие к мнимой оси и наиболее удаленные от оси корни лежат на сторонах трапеции.

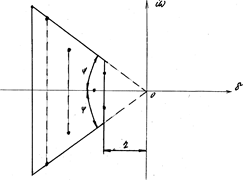
Рис.5.7

На рис.5.7 приняты следующие обозначения:

h - абсолютная величина действительной части полюса, ближайшего к мнимой оси;

y - наибольший угол, внутри и на границе которого расположены все полюсы передаточной функции.

Величина h называется степенью устойчивости САУ. Если ближайший к мнимой оси корень действительный, то степень устойчивости называется апериодической, если ближайший к мнимой оси корень комплексный, то степень устойчивости называется колебательной.

Величина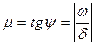называется колебательностью системы. Если все корни действительные, то колебательность равна нулю, если имеется чисто мнимый корень, то колебательность равна бесконечности, т.е. в линейной системе воз­никают незатухающие колебания,

Для определения степени устойчивости h мнимая ось на плоскости р переносится влево на величину h. Тогда характеристическое уравнение

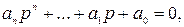(5.37)

записанное для новой переменной

z = p + h, (5.38)

принимает следующий вид:

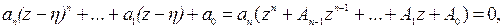(5.39)

где Ak - постоянные коэффициенты.

Уравнение (5.39) называется смещенным характеристическим уравнением. Оно имеет, по крайней мере, один мнимый корень. При этом система находится на границе устойчивости, следовательно, старший определитель Гурвица, составленный по этому уравнению, должен быть равен нулю:

∆n = ∆_n-1∙A0 = 0. (5.40)

Равенство (5.40) возможно в двух случаях.

1. ∆_n-1 = 0; A0> 0 и все остальные диагональные миноры определителя ∆n положительны.

В этом случае степень устойчивости – колебательная.

2. А0 = 0; ∆n-1 > 0 и все остальные условия устойчивости выполняются.

В этом случае уравнение (5.39) имеет один нулевой корень, следовательно, уравнение (5.37) имеет ближайший к мнимой оси корень действительный, т.е. степень устойчивости в этом случае будет апериодической.

В качестве примера рассмотрим диаграмму Вышнеградского для уравнений третьего порядка

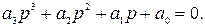
Приведя его к нормированному виду, получим

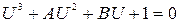, (5.41)

где ;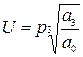

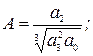
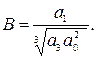
Введем новую переменную z = U + η.

Смещенное характеристическое уравнение принимает вид

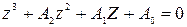
. (5.42)

Коэффициенты А0, А1 и А2 определяются по формулам:

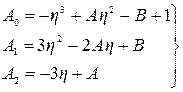
Определитель Гурвица, составленный по уравнению (5.42),имеет вид

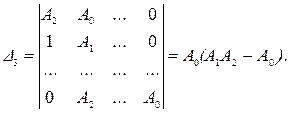
В случае апериодической устойчивости

А0 = 0; А1> 0; А2> 0,

т.е. 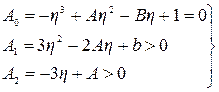. (5.43)

Система (5.43) представляет собой параметрическое уравнение прямой. Задаваясь различными значениями η на плоскости А,В можно построить линии равной степени устойчивости. Эти линии наносятся в тех областях, для которых справедливы неравенства системы (5.43). Для определения границ этих областей можно воспользоваться следующими равенствами:

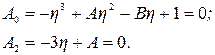
(5.44)

Система (5.44) представляет собой уравнения граничной кри­вой в неявном виде. На основании (5.44) запишем уравнения граничной кривой в параметрической форме

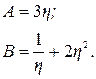
(5.45)

Уравнение (5.45) справедливо, если

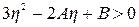. (5.46)

Граничная кривая p, построенная по уравнениям (5.45) при 0 < η < 1, показана на рис. 5.8. Для построения второй граничной кривой воспользуемся следу­ющими уравнениями системы (5.43)

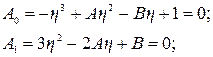
(5.47)

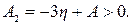(5.48)

Уравнения (5.47) граничной кривой в параметрической форме принимает вид

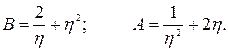
(5.49)

При А2 = -3η + А >0, т.е. при η < 1граничная кривая, построенная на плоскости А,В по уравнениям (5.49), имеет вид Q, показанный на рис. 5.8.

Граничные кривые Р и Q полностью определяют область апериодической степени устойчивости. Вышнеградский доказал, что при η ³ 1 можно построить кривую R, которая делит область апериодической степени устойчивости на две области: область между кривыми R и Q соответствует монотонному пе­реходному процессу, все корни уравнения (5.41), соответствующие этой области, – действительные.

Область между кривыми Р и R соответствует монотон­ному переходному процессу, в котором присутствует колебательная составляющая, вызванная комплексным корнем, наиболее удаленным от мнимой оси.

В случае колебательной степени устойчивости

D2 = 0; А0 > 0; A1 > 0,

т.е. 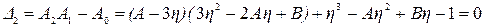(5.50)

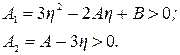
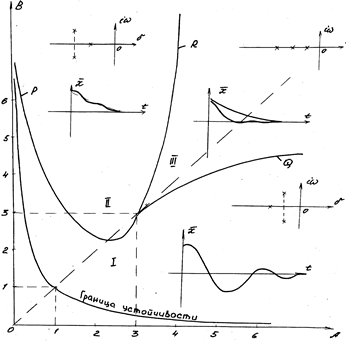
Рис. 5.8

Уравнение (5.50) в сочетании с неравенствами позво­ляет построить линии равных значений в области колебательной сте­пени устойчивости. Нетрудно показать, что граничными кривыми этой области (рис.5.8) являются гиперболы.

Наибольшая степень устойчивости h=1 имеет место в точке с координатами А=3 и В=3, следовательно, эта течка соответствует наилучшим значениям параметров с точки зрения величи­ны степени устойчивости и затухания переходного процесса.

При определении колебательности m мнимая ось поворачивается вокруг начала координат против часовой стрелки на угол (p/2-y). Диаграммы Вышнеградcкого строятся с нанесенными линиями рав­ного затухания x = соnst или линиями равной колебательности m = соnst. Колебательность и затухание связаны между собой следующими формулами:

; .

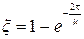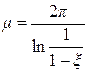Покажем это. Если 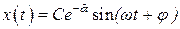, то для t = t1 имеем

.

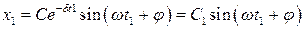
Через период T = 2p/w:

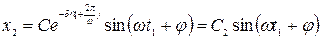
Показатель затухания

.

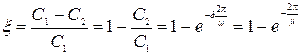Обычно в CAУ допускается затухание за один период не менее, чем 90 – 98%. Так, например, если ξ = 98%, то допустимая колебательность составит

.

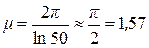Соответственно при ξ = 90% получим m = 2,73. По известным значениям m и h можно определить другие показателя качества, например, время переходного процесса

.

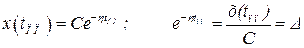Откуда при ∆ = 5 % получим

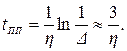
Лекция 16

План лекции:

1. Интегральные оценки качества САУ.

2. Оценки качества САУ по виду частотных характеристик.

3. Рекомендуемая литература [1, 2, 6].

5.7. ИНТЕГРАЛЬНЫЕ ОЦЕНКИ КАЧЕСТВА

Интегральные оценки относятся к аналитическим косвенным методам исследования качества САУ.

В основе метода лежат интегральные показатели, характеризующие отклонение переходного процесса реаль­ной системы от идеализированного переходного процесса. В качестве идеального принято считать ступенчатый (скачкообразный) пере­ходный процесс, протекающий мгновенно и без пере- регулирований, или процесс, представляемый экспонентой с заданными параметрами.

Интегральные оценки имеют вид определенных интегралов с пре­делами

0 ¸ ∞ от некоторых функций отклонения регулируемой величины. Наибольшее применение находят линейные и квадратичные оцен­ки.

Простейшей линейной интегральной оценкой может служить величина

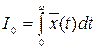, (5.51)

где 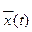– отклонение регулируемой величины x(t) от установившегося значения x уст.

В устойчивой системе 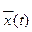→ 0 при t → ∞ и этот интеграл имеет конечную величину. Геометрически это площадь под кривой переходного процесса, построенного для отклонения (рис.5.9). Площадь будет тем меньше, чем быстрее затухает переходный процесс и чем меньше величина отклонения. Поэтому параметры систе­мы рекомендуется выбирать таким образом, чтобы добиваться минимума этой интегральной оценки.

Для вычисления интеграла (5.51) нет необходимости находить 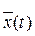, так как его можно легко вычислить, используя изображение Лапласа. Действительно, изображение Лапласа определяется выражением

.

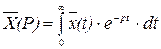Отсюда следует, что интеграл (5.51) может быть найден посред­ством предельного перехода (р → 0 ):

.

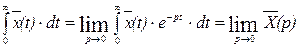Неудобством интегральной оценки вида (5.51) является то, что она годится только для монотонных процессов, когда не меняется знак отклонения 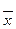. Если же имеет место колебательный процесс (рис.5.9), то при вычислении интеграла (5.51) площади будут скла­дываться алгебраически и минимум этого интеграла может соответство­вать колебаниям с малым затуханием или вообще без затухания. Так как форма переходного процесса при расчете систем регулирования может быть неизвестна, то применять интегральную оценку вида (5.51) оказывается практически нецелесообразным. Поэтому предлагается дру­гая интегральная оценка:

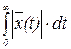(5.52)

т.е. сумма абсолютных величии всех площадей под кривой переходного процесса. Оказалось, что вычисление ее по коэффициентам уравнения затруднительно. В связи с этим целесообразно перейти к квадратичной интегральной оценке вида

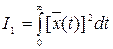, (x→0 при t→∞) (5.53)

которая не зависит от знаков отклонений, а значит, и от формы переходного процесса (монотонной или колебательной).

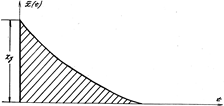
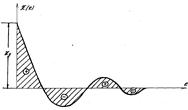
Рис. 5.9

Величина I ₁будет тем меньше, чем меньше сумма заштри­хованных на рис. 5.9 площадей (взятых для квадратов ординат), т.е. чем лучше переходный процесс приближается к идеальному скачку регулируемой величины вслед за скачком управляющего или возмущающего воздействия.

Кроме простейшей квадратичной интегральной оценки иногда применяют более сложные, которые позволяют учесть не только характер изменения 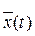, но и его производных: