Лекция 14 4 страница

4.7. ВЫДЕЛЕНИЕ ОБЛАСТЕЙ УСТОЙЧИВОСТИ

Рассмотренные выше критерии устойчивости позволяют решать в основном задачи анализа, связанные с определением устойчивости систем при всех известных параметрах. Их можно использовать и для выбора неизвестных параметров из условия устойчивости САУ. Необходимо выбирать такое значение неизвестных параметров, при котором система будет устойчивой. Однако такой подход к решению поставленной задачи связан с громоздкими вычислениями. Эта задача проще решается путем выделения в пространстве коэффициентов характеристического уравнения областей, соответствующих устойчивому состоянию системы.

Метод разбиения пространства (плоскости) коэффициентов характеристического уравнения Д(р)=0 на области устойчивости и неустойчивости называется методом Д –разбиения.

Положим, что все коэффициенты характеристического полинома

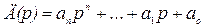
известны, кроме двух аi и aj. Требуется определить диапазон изменения этих коэффициентов, соответствующий устойчивому состоянию системы.

Для этого в плоскости неизвестных коэффициентов ai, aj можно выделить n областей, каждая из которых соответствует определенному количеству корней характеристического уравнения с отрицательными действительными частями Д(n-r) (рис. 4.14 а).

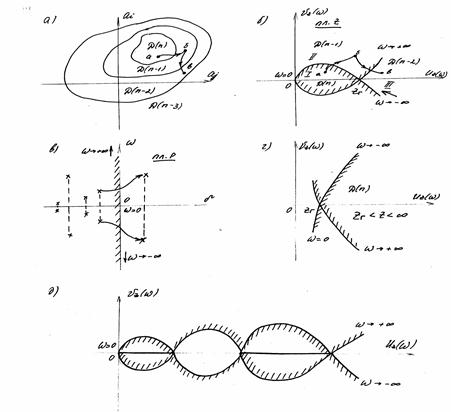
Среди этих областей можно найти область Д(n), соответствующую n левым корням, т.е. устойчивому состоянию системы.

Переход из области Д(n) в область Д(n - 1) связан с переходом одного левого корня через граничную кривую, разделяющую эти области. На плоскости комплексного переменного р (рис.4.15 в) это соответствует переходу одного из корней из левой полуплоскости в правую через мнимую ось.

Таким образом, граничную кривую в плоскости коэффициентов ai и aj можно представить себе как отображение мнимой оси плоскости р и, следовательно, записать ее уравнение в виде

Д(iw)=0. (4.31)

Уравнение (4.31) позволяет построить граничную кривую в плоскости коэффициентов характеристического уравнения.

4.7.1. Д–разбиение плоскости одного комплексного параметра

Положим, что неизвестный параметр Z системы входит в характеристическое уравнение линейно. Тогда характеристическое уравнение можно представить в виде

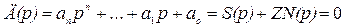, (4.32)

где S(p) и N(p) многочлены, зависящие от комплексной переменной p.

На основании (4.31) и (4.32) можно записать уравнение граничной кривой

S(iw)+ZT(iw)=0. (4.33)

Решая (4.33) относительно Z и выделяя в полученном выражении действительную Uz(w) и мнимую Vz(w) части, получим

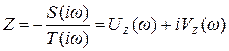. (4.34)

На основании (4.34) можно построить граничную кривую в плоскости Z при изменении частоты w=-¥¸+¥.

Учитывая четность функции Uz(w), можно ограничиться построением лишь одной ее половины при изменении частоты w =0¸¥, а затем дополнить ее симметричной половиной (рис.4.14 б).

Граничная кривая разделила плоскость Z на три области I, II, III. Среди них необходимо определить область, соответствующую устойчивому состоянию системы. Для определения этой области применяет правило штриховки, которое сводится к следующему. Мнимая ось в плоскости p и ее отображение в плоскости Uz,Vz – граничная кривая, штрихуются слева по отношению к направлению движения в сторону увеличения частоты w от -¥ до +¥. Можно предположить, что область 1, имеющая внутреннюю штриховку, соответствует левой полуплоскости p, т.е. является областью Д(n). Чтобы проверить это предположение, достаточно любое значение параметра Z, соответствующее области 1, подставить в исходное характеристическое уравнение и проверить устойчивость системы по одному из критериев. Если система окажется устойчивой для одного значения параметра Z, то она будет устойчивой и для всех остальных значений Z, лежащих внутри области Д(n).

Если с физической точки зрения параметр Z является действительным, т.е. его мнимая часть равна нулю Vz(w), то область устойчивости Д(n) вырождается в отрезок прямой, совпадающей с действительной осью (рис.4.14 б).

Полученный отрезок показывает, что система будет устойчива при изменении Z в диапазоне 0<Z<Zг, где Zг – некоторое граничное значение параметра, при котором система оказывается на границе устойчивости. При Z>Zг система становится неустойчивой.

Выбор конкретного значения параметра в диапазоне 0¸Zг производят с учетом того, как влияет этот параметр на качество и ошибки регулирования. Например, при определении общего коэффициента передачи системы выбирают его наибольшее значение, соответствующее устойчивой области, но не равное граничному значению. При этом необходимо обеспечить некоторый запас устойчивости, исключающий потерю устойчивости при изменении параметров САУ в реальных условиях.

Кроме случая, отраженного на рис 4.14 б, граничные кривые в плоскости одного параметра часто принимают вид, показанный из рис. 4.14 г, д.

ЛЕКЦИЯ 12

План лекции:

1. Д –разбиение в плоскости двух действительных параметров.

2. Суждение об устойчивости системы по ее линейной модели.

3. Рекомендуемая литература [1, 4].

Д –разбиение плоскости двух действительных параметров

Рассмотрим методику Д –разбиения плоскости двух действительных параметров для системы второго порядка.

Положим, что неизвестные параметры m и h входят в характеристическое уравнение линейно

Д(р)=mS(p)+hQ(p)+N(p). (4.35)

Уравнение граничной кривой в этом случае принимает вид

Д(iw)=mS(iw)+hQ(iw)+N(iw)=0. (4.36)

Выделяя действительную и мнимую части в уравнении (4.36) и приравнивая их к нулю, получим

mS1(w)+hQ1(w)+N1(w)=0; (4.37)

mS2(w)+hQ2(w)+N2(w)=0,

где S1(w),S2(w) и Q1(w),Q2(w) – полиномы от w.

Уравнения (4.37) решаем относительно неизвестных параметров

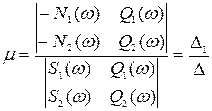; (4.38)

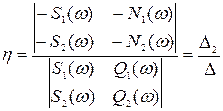, (4.39)

т.е. D1=-N1(w)Q2(w)+N2(w)Q1(w);

D2=-N2(w)S1(w)+N1(w)S2(w); (4.40)

D=S1(w)Q2(w)-S2(w)Q1(w).

Уравнения (4.38) и (4.39) является уравнениями граничной кривой в плоскости [ m;h ], которая строится при изменении частоты w oт -¥ до +¥. При этом уравнения (4.38) и (4.39) является уравнениями прямых на плоскости [ m;h ]. Их совместное решение соответствует точке пересечения этих прямых, т.е. точке граничной кривой при фиксированном значении частоты. Совокупность этих точек при различных значениях частоты и образуют граничную кривую. Если при каком-то значении частоты один из определителей (4.40) обращается в нуль, то это говорит о том, что уравнения (4.38) и (4.39) являются следствием одно другого. В этом случае вместо точки граничной кривой получается прямая, которую называют особой прямой. На плоскости параметров m и h можно построить еще две особые прямые. Уравнения этих прямых получаются путем приравнивания коэффициентов а о и а n, если они зависят от параметров m и h.

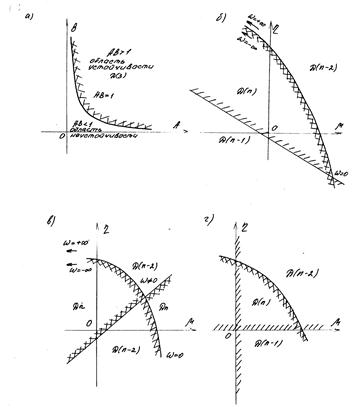
Рис. 4.15

Таким образом, в разметке областей в плоскости двух действительных параметров участвуют граничная кривая и особые прямые. Для разметки областей используют следующее правило штриховки. В направлении изменения частоты от -¥ до +¥ граничную кривую штрихуют слева, если D>0 и справа, если D<0. При w=0 определитель D, как правило, принимает нулевое значение и меняет свой знак. Через эту же точку обычно проходит особая прямая. Особые прямые штрихуют таким образом, чтобы заштрихованные стороны граничной кривой и особых прямых лежали бы друг против друга (рис. 4.15 б). Область, имеющая внутреннюю штриховку, должна соответствовать устойчивому состоянию системы. Проверку этого предположения можно выполнить так же, как и в предыдущем случае.

Некоторые особые случаи:

1. Если при w=0, D принимает нулевое значение, но не изменяет свой знак, и если через эту точку на плоскости проходит особая прямая, то она не штрихуется и при разметке областей не принимается во внимание.

2. Если при w¹0 D принимает нулевое значение и изменяет свой знак, и если через эту точку на плоскости проходит особая прямая, то она штрихуется дважды (рис.4.15,в).

3. Если D тождественно равняется нулю, то Д –разбиение плоскости двух параметров производят только особыми прямыми.

Особые прямые, участвующие в Д –разбиении, часто совпадают с осями координат (рис.4.15 г).

СУЖДЕНИЕ ОБ УСТОЙЧИВОСТИ СИСТЕМЫ

ПО ЕЕ ЛИНЕЙНОЙ МОДЕЛИ

Рассмотренные выше критерии позволяют исследовать устойчивость САУ "в малом", так как они связаны с линейными уравнениями, полученными путем линеаризации исходных нелинейных уравнений. При этом линеаризация проводилась в предположении, что переменные, характеризующие систему, имеют малые приращения.

С помощью указанных критериев мы не можем судить об устойчивости системы "в большом" или о "неограниченной устойчивости".

Рассмотрим один из методов, который позволяет судить об устойчивости систем "в большом". Положим для простоты, что уравнение возмущенного движения исследуемой системы содержит всего одну однозначную нелинейную функцию

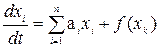. (4.41)

Производя линеаризацию функции f(x_k), ее можно заменить линейной функцией

f(xk)»cx_k, (4.42)

где c – постоянный коэффициент.

C учетом (4.42) уравнение (4.41) принимает вид

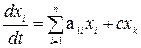. (4.43)

Методом Д –разбиения можно определить диапазон изменения с*<c<c**, соответствующий устойчивому состоянию системы (с* и с** соответствуют границе устойчивости линейной модели).

Выберет такие значения cо, c1, c2, чтобы выполнялось следующее неравенство:

c*<c1<cо<c2<c**, (4.44)

где cо – численное значение коэффициента c, полученное в результате линеаризации функции f(x_k).

В плоскости нелинейной функции f(x_k) построим исходную нелинейную функцию и два луча c₁x_k и c₂x_k т.е.

В результате такого построения могут встретиться три случая, показанные на рис.4.16.

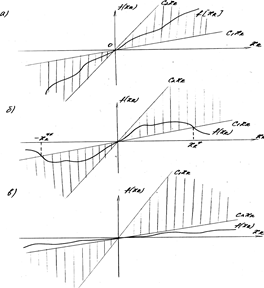
Для них можно сделать следующие выводы об устойчивости исходной нелинейной системы по ее линейной модели:

1. Если нелинейная функция f(x_k) заключена между лучами c₁x_k и c₂x_k во всем диапазоне изменения x_k (рис.4.16 а), то исходная нелинейная система неограниченно устойчива.

2. Если нелинейная функция f(x_k) заключена между лучами c₁x_k и c₂x_k лишь в окрестности начала координат при –x_k*<x_k<x_k** (рис.4.16 б), то нелинейная система устойчива "в малом".

Если реальные отклонения переменной xk не превышают ÷ x_k* ÷, то можно считать, что исходная нелинейная система устойчива "в большом".

3. Если нелинейная функция f(x_k) не заключена между лучами c₁x_k и c₂x_k даже в окрестности начала координат, то по линейной модели нельзя установить устойчивость исходной нелинейной системы даже “в малом”.

Рассмотренный метод может быть применен также в том случае, когда нелинейная функция зависит от нескольких переменных, а система содержит переменные параметре. Применение метода возможно лишь для системы, уравнения которой (4.41) содержат линеаризуемые функции.

5. КАЧЕСТВО САУ

Лекция 13

План лекции:

1. Рассказать об основных показателях качества САУ.

2. Методы построения переходных характеристик.

3. Рекомендуемая литература [1, 2, 4, 7].

5.1. ОСНОВНЫЕ ПОКАЗАТЕЛИ КАЧЕСТВА

Устойчивость является необходимым, но не достаточным условием нормальной работы САУ. В устойчивой системе могут возникать собственные колебания с недопустимо большой амплитудой и временем затухания. О качестве регулирования судят по поведению систем в переходном режиме, т.е. при переходе САУ из одного установившегося состояния в другое.

Показатели качества чаще всего определяются по виду переходной характеристики, т.е. по графику переходного процесса, построенному при единичном ступенчатом воздействии на систему:

.

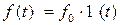В следящих системах иногда задают воздействия, изменяющиеся во времени с постоянной скоростью или постоянным ускорением.

К основным показателям качества относят время переходного процесса t_ПП , пере­регулирование σ%, максимальное отклонение регулируемой величины х_m, установившееся значение регулируемой величины х_у или статическую ошибку, полосу пропускания ω_п и др.

1. Время переходного процесса t_ПП характеризует быстродействие системы и определяется как интервал времени от начала переходного процесса до момента, когда отклонение выходной величины от ее нового установившегося значения становятся меньше определенной достаточно малой величины. Обычно в качестве последней берут 5% максимального отклонения в переходный период (рис. 5.1 в).

2. Максимальное отклонение в переходный период. В случае переходного процесса, вызванного возмущением, максимальное отклонение определяется величиной х_m, приходящейся на единицу возмущения f = 1 (t). В случае переходных процессов, вызванных изменением задающего воздействия, максимальное отклонение определяется относительно нового установившегося значения х_у и равно в процентах

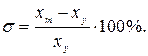
Заметим, что эта величина аналогична предыдущей, поскольку здесь х_у пропорционально задающему воздействию. Величина σ часто называется перерегулированием.

3. Колебательность переходного процесса оценивают отношением соседних максимумов х_m1/ х_m2 в процентах.

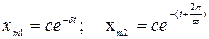
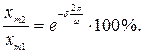
Незатухающие колебания имеют колебательность 100%. Колебательность стремится к нулю при уменьшении до нуля второго максимума переходной характеристики, когда получается неколебательный процесс.

Иногда колебательность определяется числом колебаний, равным числу минимумов кривой переходного процесса в интервале времени.

Приемлемым числом колебаний в САУ считается 1–2, иногда допускается 3 и более колебаний.

4. Установившееся значение регулируемой величины х_у зависит от астатизма САУ. В астатических системах установившаяся ошибка равна нулю и установившееся значение регулируемой величины будет равно её заданному значению, т.е. управляющей величине. В статических системах установившееся значение регулируемой величины будет отличаться от её заданного значения на величину установившейся ошибки.

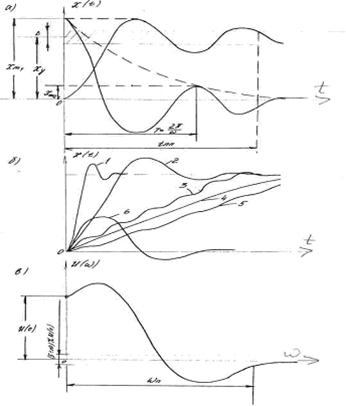
Рис. 5.1

Установившаяся ошибка в статической системе х_ст зависит от величины входного воздействия f₀ и от коэффициента передачи системы k.

Для задающего воздействия

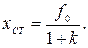
Для возмущающего воздействия

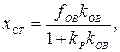
где k_o6 – коэффициент передачи объекта регулирования; k_р – коэффициент передачи регулятора.

Относительная величина установившейся ошибки называется коэффициентом статизма системы и определяется по формуле

.

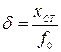Коэффициент статизма системы относительно задающего воздействия определяется выражением

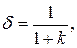
а относительно возмущающего воздействия имеет вид

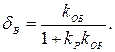
5. Показателем качества может служить также характер переходного процесса (монотонный или колебательный). Переходный процесс считается монотонным, если производная от регулируемой величины по времени 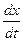не меняет знак. На рис. 5.1 б показаны примеры колебательных (1, 2, 3, 6) и монотонных (4, 5) переходных процессов.

Полоса пропускания системы ω_П определяется диапазоном частот внешних воздействий, проходящих через систему с той или иной степенью искажения. Полосу пропускания определяют по частотным характеристикам, например, по вещественной характеристике системы (рис. 5.1 в).

5.2. МЕТОДЫ ПОСТРОЕНИЯ ПЕРЕХОДНЫХ ПРОЦЕССОВ

Все современные методы анализа качества переходного процесса регулирова­ния можно разделить на две основные группы.

К первой группе относятся методы непосредственного решения (интегриро­вания) тем или иным способом дифференциальных уравнений системы и выполне­ния согласно этому решению графического построения переходного процесса. Это прямые методы анализа. Они являются наиболее точными при исследовании качественных показателей системы. Однако эти методы становятся трудоемкими для дифференциальных уравнений высоких порядков, особенно если при этом требуется выяснить влияние тех или иных параметров системы на переходный процесс. Та­кие задачи аффективно решаются с применением вычислительных машин путем мо­делирования системы.

Ко второй группе относятся методы, позволяющие (в той или иной мере) обойти громоздкие вычислительные операции. Это косвенные методы анализа, не требующие построения кривой переходного процесса.

Рассмотрим первую группу методов. Практическое применение при реше­нии дифференциальных уравнений в ТАУ нашли методы преобразования Лапласа и Фурье.

Преобразование Лапласа является функциональным и служит для преобразования функций вещественной переменной в функции комплексной пере­менной.

Построение переходного процесса с помощью преобразований Лапласа можно свести к двум этапам:

1. По известным дифференциальным уравнениям САУ и известному внешнему воздействию f(t) определяют изображение регулируемой величины

,

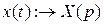которое представляют обычно в следующей форме:

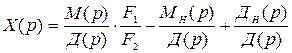. (5.1)

2. По найденному изображению (5.1) на основании формул обратного преобразования Лапласа определяют зависимость регулируемой величины от времени x(t) при заданном внешнем воздействии f(t), например, полагают, что

.

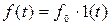В общем случае x(t) можно представить в виде составляющих

х(t)= х_С (t)+х_В (t).

Метод, основанный на преобразованиях Лапласа, практически не имеет ограничений, позволяет анализировать как собственные, так и вынужденные колебания САУ в переходном режиме. Недостаток метода связан с необходимо­стью определения корней характеристического уравнения.

Преобразования Фурье также являются функциональными, так как они преобразуют некоторую функцию переменного t в совершенно иную функцию переменного w, и наоборот.

Преобразования Фурье имеют вид:

X(iω)= 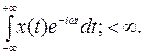(5.2)

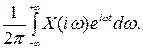x(t)= (5.3)

Интегральное уравнение (5.2) называется прямым, а уравнение (5.3) - об­ратным преобразованием Фурье.

Интеграл Фурье (прямое преобразование Фурье) позволяет разложить непериодическую функцию x(t), обладающую свойством абсолютной интегрируе­мости в заданных пределах, в бесконечный ряд гармоник, образующих непрерыв­ный спектр частот в интервале от - ∞ до +∞ с бесконечно малым интервалом частот между смежными гармониками (т.е. в пределе ∆→0).

Метод преобразования Фурье непригоден при ненулевых начальных (или граничных) условиях. Этот метод может применяться лишь тогда, когда искомые функции имеют изображение Фурье, т.е. для абсолютно интегрируемых функций времени, удовлетворяющих неравенству

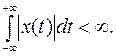(5.4)

Наиболее часто встречающимися в ТАУ функциями яв­ляются единичная ступенчатая функция и произведение синусоидальной функции на единичную функцию. Преобразование Фурье неприменимо ни к одной из этих функций, так как не удовлетворяется условие (5.4).

При исследовании качества САУ преобразование Фурье может использо­ваться для анализа собственных колебаний заведомо устойчивой системы, т.к. в этом случае при 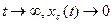и условие (5.4) выполняется.

С учетом (5.3) будем иметь

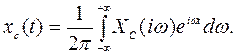(5.5)

5.2.1. Частотный метод анализа качества САУ,

основанный на преобразовании Фурье

Выделяя действительные и мнимые части функций

X_С (iω) = U_С (ω)+ i V_С (ω),

выражение (5.5) перепишем в виде

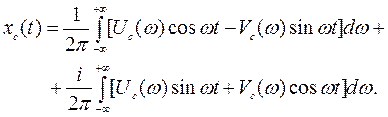
Учитывая четность функций U_С (ω) и cos ωt и нечетность функций V_С (ω) и sin ωt, получим

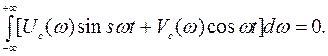
Тогда

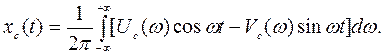(5.6)

Полагая, что при t < 0 x_c (t) = 0, можно записать

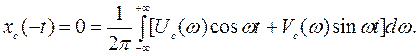(5.7)

В результате сложения (5.6) и (5.7) получим

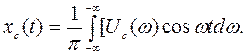(5.8)

Учитывая четность подынтегральной функции, выражение (5. 8) принимает вид

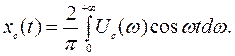(5.9)

В результате вычитания (5.6) из (5.7) получим

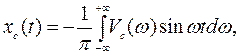
или 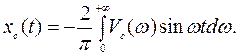(5.10)

Найдем зависимость функций Uc(ω) и Vc(ω) от действительной U(ω) и мнимой V(ω) частей АФЧХ Ф(iω) замкнутой системы.

На основании теоремы операционного исчисления о предельном значении функции можно записать

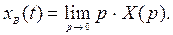
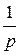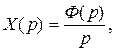Если f (t) = l (t), т.е. F(p) = и то

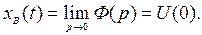(5.11)

Тогда

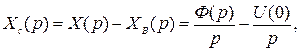
или

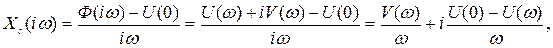
т.е.

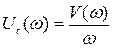; (5.12)

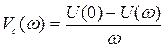. (5.13)

На основании (5.9) с учетом (5.12) будем имееть

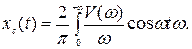(5.14)

На основании (5.10) с учетом (5.13):

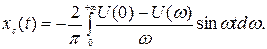(5.15)

Полное движение системы x(t)= x_С (t) + x_B (t).

Учитывая (5.1 1) и (5.15), получим

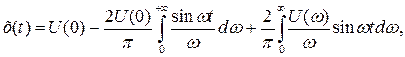
где 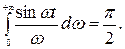(Табличный интеграл).

С учетом этого

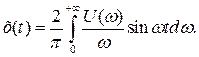(5.16)

Формула (5.16) связывает функцию x(t) с U(ω). Она позволяет вычислить координаты графика переходного процесса по известным значениям вещественной частотной характеристики. Иногда пользуются приближенным методом построения переходного процесса с помощью трапеции­дальных частотных характеристик..

Приближенный метод построения кривой переходного процесса с помощью трапециидальных частотных

характеристик

В выражении (5.16) производят следующую замену:

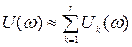, (5.17)

где U_k(ω) - трапеции, две стороны которых совпадают с осями координат;

r - количество трапеций, на которые разбивается вещественная характеристика U(ω).

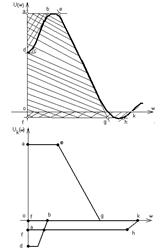
Замена (5.17) соответствует аппроксимации вещественной частотной харак­теристики U(ω) суммой трапеций (рис. 5.2 а). При этом суммарная площадь трапеций (с учетом их знаков) должна быть приблизительно равна площади под кривой вещественной характеристики.

Кривая переходного процесса системы строится в результате сложения переходных процессов x_к (t), соответствующих k- м трапециям.

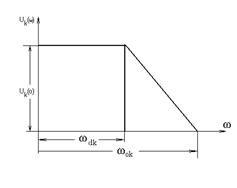
Каждая из трапеций характеризуется следующими координатами τ_ok, ω_dk, ω_ok

(рис. 5.2 б) и относительной величиной

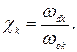
Существуют таблицы h -функций для единичных трапеций с различными коэффициентами наклона χ.

а б

Рис. 5.2

Кривая переходного процесса получается суммированием построенных h -функций с учетом правил масштабов, которые заключаются в следующем.

1. Перед сложением ординату каждой h -функции необходимо умножить на высоту соответствующей трапеции (с учетом знака).

2. Перед сложением необходимо изменить масштаб времени каждой h -функции в соответствии с теоремой подобия.

Действительное время равно времени t, приведенному в таблице h(τ) функций, деленному на частоту среза соответствующей трапециидальной характеристики:

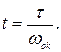
План лекции:

1. Рассказать о построении вещественной частотной характеристики.

2. Построение частотных характеристик замкнутых систем по передаточным функциям разомкнутой системы.

3. Рекомендуемая литература [1, 8 ].

5.3. ПОСТРОЕНИЕ ВЕЩЕСТВЕННОЙ ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ ЗАМКНУТОЙ СИСТЕМЫ ПО ЧАСТОТНЫМ ХАРАКТЕРИСТИКАМ

РАЗОМКНУТОЙ СИСТЕМЫ

Вещественную частотную характеристику можно построить по АФЧХ, ЛАФЧХ замкнутой и разомкнутой системы. Рассмотрим построение вещественной частотной характеристики замкнутой системы по АФЧХ разомкнутой системы. Структурную схему системы можно представить в виде, показанном на рис. 5.3.