Реализация булевых функций формулами

В этом параграфе мы обсудим ряд важных понятий, которые обычно опускаются, потому как считаются самоочевидными. Такими понятиями являются, в частности, реализация функций формулами, интерпретация формул для вычисления значений функций, равносильность формул, подстановки и замены в формулах. Между тем именно программная реализация работы с функциями требует учета некоторых тонкостей, связанных с данными понятиями, которые необходимо обсудить. Роль этих тонких понятий особенно возрастает в формальных теориях, в которых нужно четко различать понятия.

Начнем по порядку. Можно определить булеву функцию способом табличного задания. Этот способ является самой прямой реализацией понятия отображения (функции) элементов одного множества в другое. Этот способ применим только для конечных множеств, да и то с ростом числа переменных он становится необозримым.

Но существует и другой способ задания функций – и не только булевых. Уже в элементарной математике можно получать новые функции, подставляя одни из них в качестве аргументов в другие. Здесь принцип тот же самый, не зря ранее были перечислены все 16 функций от двух переменных, и большинству из них были присвоены собственные имена и обозначения. Принцип же построения функций основан на том, что любая булева функция, как и её аргументы, является элементом множества В, что позволяет каждую функцию снова подставлять в качестве аргументов в другие функции, тем самым получая всё новые и новые функции. Понятно, что в качестве «кирпичиков» можно использовать совершенно разные функции – мы этот вопрос впоследствии будем подробно обсуждать – но в настоящее время мы ограничимся только некоторыми из поименованных двухместных функций и одноместных – тождественной и отрицания, а также, конечно, 0 и 1.

Определим, что такое формула. Пусть заданы: набор переменных X = {x₁, x₂,…, x_n, …} и некоторое фиксированное множество функций F = {f₁, f₂, …, f_m}. Эти два множества в совокупности называют алфавитом, причём XÈF =Æ.

Формулой, или суперпозицией над F называется выражение: Ф _F = f(t₁, t₂,…, t_n), где fÎF и t_i либо переменная, либо формула над F. f называется внешней (главной) формулой, а t_i называются подформулами. Множество F называют также базисом.

Это определение формулы является общим для всей математики. – Ср. терм.

В данном определении неявно присутствуют две операции: операция подстановки формул в формулу (суперпозиции) и операция замены переменных. Если в базисе нет проектирующей (тождественной) функции, то эти операции следует рассматривать отдельно.

Множество всех формул над F называется замыканием F и обозначается [F].

Глубина/сложность формулы определяется индуктивно следующим образом:

1. Переменные являются формулами глубины/сложности 0.

2. Глубина формулы f(t₁, t₂,…, t_n) есть k+1, где k есть максимальная глубина входящих в нее подформул t_i; сложность формулы f(t₁, t₂,…, t_n) есть 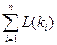, где L (k_i) есть сложность входящих в нее подформул t_i.

В силу исключительной важности понятия формулы, дадим его еще раз в несколько отличной форме – имея в виду именно булеву алгебру. Изменения касаются, в основном, формы записи формул (инфиксной).

Дан алфавит А, являющийся объединением четырех алфавитов: A₁={0,1} – константы, A₂={x,y,…,х₁,…} – переменные, A₃={,&,Ú,→, ~, |, ↓,…} – символы логических операций (связки), т.е. обозначения элементарных булевых функций, A₄={),(} – вспомогательные символы. Формулы над алфавитом А (или, если угодно, над А₃) строятся следующим образом:

1. Все константы и переменные – формулы (глубины 0).

2. Если Ф – формула, то Ф – формула.

3. Если Ф₁ и Ф₂ – формулы, то (Ф₁&Ф₂), (Ф₁ÚФ₂), (Ф₁→Ф₂), (Ф₁~Ф₂), (Ф₁|Ф₂), (Ф₁↓Ф₂), … – формулы.

4. Других формул нет.

Это определение конкретизирует общее: задаётся базис – множество элементарных булевых функций, символы констант и переменных и служебные символы.

Перейдем к следующему вопросу: как соотносятся между собой функции и формулы? С одной стороны, понятно, что в произвольную формулу входит конечное число переменных и, придавая им определенные значения, можно по подформулам выбраться «наверх», на каждом шаге составляя таблицу истинности (или Кэли) – на последнем шаге придем к таблице истинности для внешней формулы. – Итак, в одну сторону соответствие есть – каждой формуле соответствует вполне определенная булева функция. С другой стороны, представляется, что формул можно построить значительно больше, чем существует разных булевых функций от фиксированного числа переменных. Но раз формул больше, то соответствие нескольких формул одной булевой функции приводит к следующему: если Ф₁ соответствует f (обозначим Ф₁Þ f), и в то же время Ф₂ соответствует f, то эти соответствия порождают отношение между Ф₁ и Ф₂, которое, как легко проверяется, является отношением эквивалентности и, следовательно, разбивает все множество формул на непересекающиеся классы эквивалентности.

Это отношение эквивалентности называется равносильностью формул. Мы его будем в дальнейшем обозначать знаком ≡: Ф₁≡Ф₂. Таким образом, с учетом операции эквиваленции ~, мы получили уже три понятия и три знака, описывающих эти понятия, близких понятию равенства: =, ~ и ≡. Разница последних двух понятий заключается в том, что одно их них (~) есть (базисная) операция булевой алгебры, определяющая формулы, в то время как другое (≡) не является операцией над формулами, а привнесено извне, через булевы функции.

Аналогия, далёкая от математики: корова и кошка – домашние животные. Понятие «домашний» не является внутренней, биологической характеристикой объектов, а указывает на отношение к ним некоторого внешнего субъекта. В случаях, когда существуют иерархические отношения типа объект–субъект, отношения субъекта принято снабжать приставкой «meta»: метаэквиваленция, метаимпликация и т.д., подчеркивая их происхождение извне рассматриваемой теории.

Выяснение связи эквиваленции и равносильности составляет уже предмет математической логики.