После правильно выбранного направления 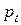 , в градиентных алгоритмах обучения, следует определить новую точку решения
, в градиентных алгоритмах обучения, следует определить новую точку решения  , в которой будет выполняться условие
, в которой будет выполняться условие 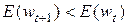 . Необходимо подобрать такое значение
. Необходимо подобрать такое значение 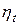 , чтобы новое решение
, чтобы новое решение 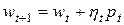 лежало как можно ближе к минимуму функции E(w) в направлении
лежало как можно ближе к минимуму функции E(w) в направлении 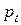 . Грамотный подбор коэффициента
. Грамотный подбор коэффициента 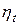 оказывает огромное влияние на сходимость алгоритма оптимизации к минимуму целевой функции. Чем сильнее величина
оказывает огромное влияние на сходимость алгоритма оптимизации к минимуму целевой функции. Чем сильнее величина 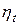 отличается от значения, при котором E(w) достигает минимума в выбранном направлении
отличается от значения, при котором E(w) достигает минимума в выбранном направлении 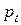 , тем большее количество итераций потребуется для поиска оптимального решения. Слишком малое значение
, тем большее количество итераций потребуется для поиска оптимального решения. Слишком малое значение 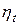 не позволяет минимизировать целевую функцию за один шаг и вызывает необходимость повторно двигаться в том же направлении. Слишком большой шаг приводит к «перепрыгиванию» через минимум функции и фактически заставляет возвращаться к нему.
не позволяет минимизировать целевую функцию за один шаг и вызывает необходимость повторно двигаться в том же направлении. Слишком большой шаг приводит к «перепрыгиванию» через минимум функции и фактически заставляет возвращаться к нему.
Существуют различные способы подбора значений 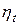 , называемого в теории нейронных сетей коэффициентом обучения. Простейший из них основан на фиксации постоянного значения
, называемого в теории нейронных сетей коэффициентом обучения. Простейший из них основан на фиксации постоянного значения 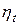 на весь период оптимизации. Этот способ практически используется только совместно с методом наискорейшего спуска. Он имеет низкую эффективность, поскольку значение коэффициента обучения никак не зависит от вектора фактического градиента и, следовательно, от направления p на данной итерации. Величина h подбирается, как правило, раздельно для каждого слоя сети с использованием различных эмпирических зависимостей. Один из походов состоит в определении минимального значения h для каждого слоя по формуле
на весь период оптимизации. Этот способ практически используется только совместно с методом наискорейшего спуска. Он имеет низкую эффективность, поскольку значение коэффициента обучения никак не зависит от вектора фактического градиента и, следовательно, от направления p на данной итерации. Величина h подбирается, как правило, раздельно для каждого слоя сети с использованием различных эмпирических зависимостей. Один из походов состоит в определении минимального значения h для каждого слоя по формуле
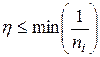 , (3.4)
, (3.4)
где 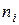 обозначает количество входов i-го нейрона в слое.
обозначает количество входов i-го нейрона в слое.
Наиболее эффективный, хотя и наиболее сложный, метод подбора коэффициента обучения связан с направленной минимизацией целевой функции в выбранном заранее направлении 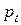 . Необходимо так подобрать скалярное значение
. Необходимо так подобрать скалярное значение 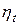 , чтобы новое решение
, чтобы новое решение 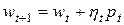 соответствовало минимуму целевой функции в данном направлении
соответствовало минимуму целевой функции в данном направлении 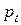 . В действительности получаемое решение
. В действительности получаемое решение  только с определенным приближением может считаться настоящим минимумом. Это результат компромисса между объемом вычислений и влиянием величины
только с определенным приближением может считаться настоящим минимумом. Это результат компромисса между объемом вычислений и влиянием величины 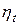 на сходимость алгоритма.
на сходимость алгоритма.
Опишем метод аппроксимации целевой функции E(w) в предварительно выбранном направлении 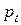 с последующим расчетом минимума, получаемого таким образом, функции одной переменной h. Выберем для аппроксимации многочлен второго порядка вида
с последующим расчетом минимума, получаемого таким образом, функции одной переменной h. Выберем для аппроксимации многочлен второго порядка вида
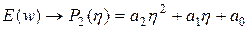 , (3.5)
, (3.5)
где 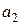 ,
, 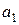 и
и 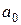 обозначены коэффициенты, определяемые в каждом цикле оптимизации. Выражение (3.5) – это многочлен P2 одной скалярной переменной h. Если для расчета входящих в P2 коэффициентов используются три произвольные точки
обозначены коэффициенты, определяемые в каждом цикле оптимизации. Выражение (3.5) – это многочлен P2 одной скалярной переменной h. Если для расчета входящих в P2 коэффициентов используются три произвольные точки 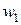 ,
, 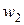 и
и 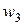 , лежащие в направлении
, лежащие в направлении 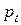 , т.е.
, т.е. 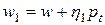 ,
, 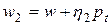 ,
, 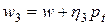 (в этом выражении w обозначено предыдущее решение), а соответствующие этим точкам значения целевой функции E(w) обозначены
(в этом выражении w обозначено предыдущее решение), а соответствующие этим точкам значения целевой функции E(w) обозначены 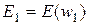 ,
, 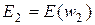 ,
, 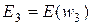 , то
, то
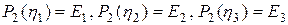 . (3.6)
. (3.6)
Коэффициенты 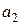 ,
, 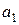 и
и 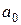 многочлена P2 рассчитываются в соответствии с системой линейных уравнений, описываемых в (3.6). Для определения минимума этого многочлена его производная
многочлена P2 рассчитываются в соответствии с системой линейных уравнений, описываемых в (3.6). Для определения минимума этого многочлена его производная 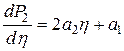 приравнивается к нулю, что позволяет получить значение h в виде
приравнивается к нулю, что позволяет получить значение h в виде 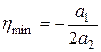 . После подстановки выражений
. После подстановки выражений 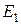 ,
, 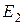 и
и 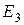 в формулу расчета
в формулу расчета 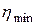 получаем:
получаем:
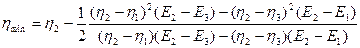 (3.7)
(3.7)
Применение градиентных методов, в которых кроме значения функции учитывается и её производная вдоль направляющего вектора 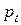 , позволяют значительно ускорить достижение минимума, так как используют информацию о направлении уменьшения величины целевой функции. В этом случае применяется аппроксимирующий многочлен третьей степени:
, позволяют значительно ускорить достижение минимума, так как используют информацию о направлении уменьшения величины целевой функции. В этом случае применяется аппроксимирующий многочлен третьей степени:
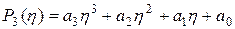 (3.8)
(3.8)
Значения четырёх коэффициентов 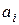 этого многочлена можно получить исходя из информации о величине функции и её производной в двух точках. Если приравнять к нулю производную многочлена относительно
этого многочлена можно получить исходя из информации о величине функции и её производной в двух точках. Если приравнять к нулю производную многочлена относительно 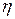 , то можно получить формулу для расчёта
, то можно получить формулу для расчёта 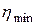 в виде:
в виде:
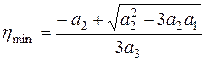 (3.9)
(3.9)
 2014-02-02
2014-02-02 1109
1109
