Лекция 3. Положения, лежащие в основе линеаризации

Положения, лежащие в основе линеаризации.

Линеаризация заключается в переходе к линейному дифференциальному уравнению, переменные которого являются отклонениями от некоторого номинального режима, удовлетворяющего уравнению (**).

Вычислим дифференциал F, введя предварительно следующие обозначения:

Z = (y¢, y¢¢,... y⁽ⁿ⁾)

U = (u¢, u¢¢,... u^(m))

F(Z,U)=0 (**)

Пусть Z_н и U_н - номинальная траектория, удовлетворяющая (**)

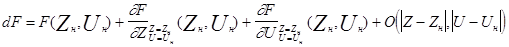
т.к. траектория номинальная:

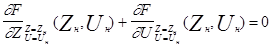(2)

- линеаризованное уравнение.

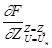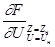При этом и - коэффициенты ряда Тейлора.

Введем: x = y-y_н

и u = u-u_н

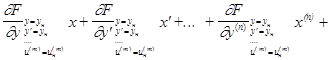
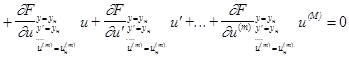(3)

Так как все частные производные представляют из себя либо постоянные матрицы, либо, в крайнем, случае матрицы зависящие только от времени, то полученное уравнение (3) есть либо система линейных дифференциальных уравнений с постоянными коэффициентами, относительно отклонений x и u, либо система с переменными коэффициентами. Постоянность или переменность зависит от номинальной траектории. В частности, в системах стабилизации, где номинальные траектории - константы, получаются постоянные матрицы.

Таким образом, перейдя к уравнениям в отклонениях, мы получаем систему линейных дифференциальных уравнений, которую рассматриваем относительно выходной величины, т.е. порядок этой системы линейных дифференциальных уравнений равен n по порядку производной при x.

Дифференцирование же входного сигнала u рассматривается не как дифференциальное уравнение относительно u, а как операция с известным входным сигналом.

Соберем все коэффициенты дифференциальных уравнений в матрицы и получим окончательно следующую матричную систему:

A₀(t)x + A₁(t)x+…+A_n(t)x=B₀(t)U+…+B_m(t)U

Если удаётся удачно выбрать номинальную траекторию (это зависит не только от мастерства исследователя, но и от самой задачи), матрицы А_i и B_i становятся постоянными. И для такой системы линейных дифференциальных уравнений с постоянными коэффициентами можно получить до конца точное решение и полностью его исследовать. В случае постоянных коэффициентов система называется стационарной.

Чаще всего оказывается, что входные и выходные величины объекта - скалярные функции u b x:

a₀x⁽ⁿ⁾+…+a_nx=b₀u^(m)+…+b_mu (4)

(4) – описывает стационарный объект с одним входом и одним выходом.

Переход от дифференциального уравнения порядка n к системе из n -дифференциальных уравнений 1-го порядка

Вводим дополнительные переменные (x₁……x_n), равные производным х.

x⁽ⁿ⁾= -1/a₀ (a₁x^(n-1)+…a_nx-b₀u^(m)-…b_mu)

Вводим: х=c^т *(x₁……x_n), здесь с-вектор констант, позволяющий вычислить х из

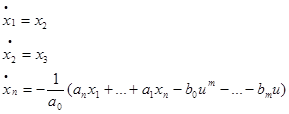
вектора (x₁……x_n)

(5)

Начальные условия для x(t) переходят в начальные условия для (x₁……x_n).

Получившаяся система дифференциальных уравнений (5) может быть записана в матричном виде следующим образом:

введем вектор

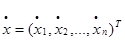
И (5) выражается:

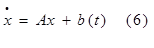
Тогда:

Отметим, что настоящий выход объекта равен х₁, то есть можно записать, что при с=(1 0 0 0 …0) х₁= с^т* (х₁ …….х _n).

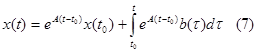
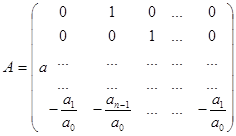
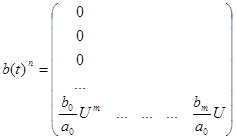
Решение системы уравнений (6)всегда может быть записано в следующем виде:

Где первое слагаемое – решение однородного уравнения, второе – неоднородного.

Формула (7) справедлива вне зависимости от порядка исходного дифференциального уравнения.

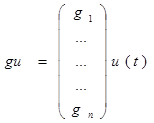
Заключение: В правую часть уравнения (6) входят производные от управляющего воздействия. Можно показать, что от этих производных можно избавиться. Они будут вычисляться “автоматически” в процессе решения системы уравнений,и выглядит это след. образом: нужно вместо b(t) взять

Коэффициенты g₁ и g_n вычисляем по следующей формуле:

g₀=0

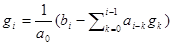
Это рекуррентная формула в том смысле, что g вычисляется последовательно.

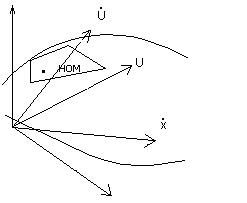
Пример и геометрическая интерпретация линеаризации.

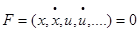
Есть не что иное, как уравнение поверхности в пространстве. Координат столько, сколько аргументов у функции. Номинальная траектория есть просто точка на поверхности, линеаризованное уравнение (2) – уравнение касательной плоскости