Тройной интеграл. Св-ва. Сведение к повторному интегралу. Замена переем-х. Цилиндр-е и сфер-е коорд-ты. Приложения тройного интеграла.
Приложения двойных интегралов.
1) Масса плоской пластинки.
Поверхностная плотность 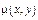 .
.

Элемент массы равен 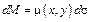 .
.
Масса всей пластинки равна 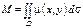 .
.
2) Статические моменты инерции и центр тяжести пластинки.
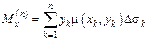 ,
, 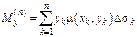 .
.
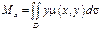 ,
, 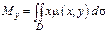 .
.
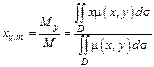 ,
, 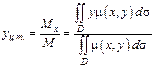 .
.
3) Моменты инерции пластинки.
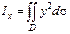 ,
, 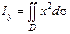 .
.
Центробежный момент инерции
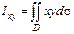 .
.
Полярный момент инерции относ-но оси 
 .
.
Рассмотрим тело объемом 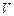 переменной плотности
переменной плотности 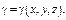
Разобьем тело произвольным образом на 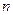 частей элементарными объемами
частей элементарными объемами 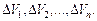 Выберем в каждом из элемент-х объемов произв-ю точку
Выберем в каждом из элемент-х объемов произв-ю точку 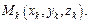 Масса элем-го объема приближенно равна
Масса элем-го объема приближенно равна 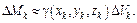
Просуммируем массу всех элементарных объемов
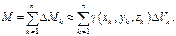
Выраж-е в правой части наз-ся интегр-й суммой. Устремим наиб-й диаметр элем-х объемов к 0 и рассмотрим предел 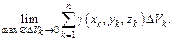
Если этот предел интегр-й суммы сущ-ет, то, очевидно, он равен массе тела и наз-ся тройным интегралом от ф-и 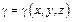 по объему
по объему 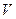
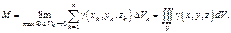
Вообще, тройным интегралом от ф-и  по объему
по объему 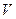 наз-ся предел интегральной суммы
наз-ся предел интегральной суммы
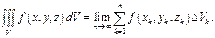
Св-ва двойных интегралов переносятся на тройные интегралы:
1) 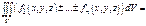
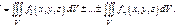
2) 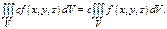
3) 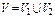 ,
, 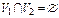 . Тогда
. Тогда 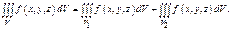
4) Если "(x,y,z)ÎV 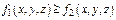 , то
, то 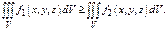
5) Если 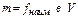 ,
, 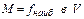 , то
, то 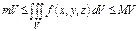 , где
, где 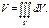
6) 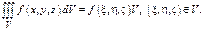
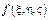 - среднее знач-е f в области V.
- среднее знач-е f в области V.
1) Декартовы коорд-ты. Пусть дан тройной интеграл 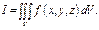
Разобьем область интегрирования 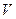 на элементарные объемы плоскостями, парал-ми корд-ым плоскостям. Тогда элементарный объем равен
на элементарные объемы плоскостями, парал-ми корд-ым плоскостям. Тогда элементарный объем равен 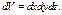 Следов-но
Следов-но 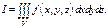
Установим правило вычисления тройного интеграла
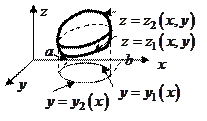

Пример. Вычислить тройной интеграл 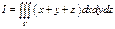 по обл-ти, огранич-й плоск-ми:
по обл-ти, огранич-й плоск-ми: 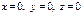 и
и 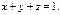 Построим область интегрирования:
Построим область интегрирования:
|
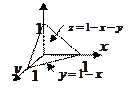
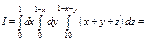
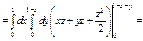
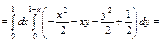
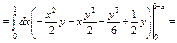

 2014-02-02
2014-02-02 561
561