П.1. Постановка задачи

Необходимо решить ДУ и СДУ на некотором наперёд заданном интервале с наперёд заданной точностью, либо оценить погрешность, которая найдена решением.

В ЧМ мы ищем только частные решения ДУ.

П.2. Простейший вариант задачи.

Простейший метод её решения – метод Эйлера.

Имеем ДУ 1-го порядка, а вместе с ним одно начальное условие:

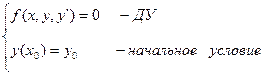(Задача Коши)

В дальнейшем всегда будем рассматривать ДУ, разрешенное относительно старшей производной, т.е. вида:

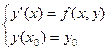(6.1)

Общая идея всех методов численного решения ДУ и СДУ:

Фиксируем шаг h и будем находить по некоторым специальным формулам

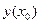- задан, 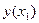, ,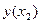…, , 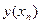где 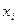- равностоящие точки, а 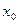,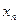-границы интервала [a,b], на котором нам необходимо найти решение ДУ.

При этом, необходимо брать шаг h достаточно малым, с тем, чтобы погрешность была невелика.

Простейший метод решения ДУ – метод Эйлера:

Заметим, что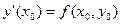- величина нам известная. Заменим неизвестное нам решение ДУ на касательную, а именно: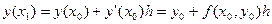

В общем виде: 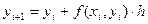(формула Эйлера).

Геометрическая интерпретация метода Эйлера:

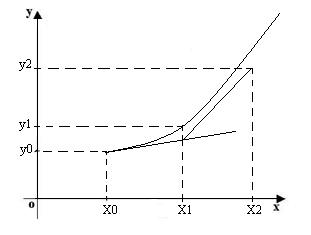
Локальная погрешность метода Эйлера: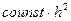

П.3.Простейшая модификация метода Эйлера – метод Рунге-Кутта 2-го порядка.

Заменим приращение функции на первом шаге 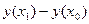не на 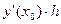, как делали в методе Эйлера, а на более точное значение - на значение производной в середине интервала 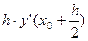. А для того, чтобы найти .

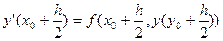Заменим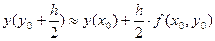

Окончательно получаем следующую формулу:

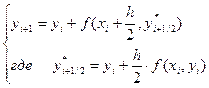
(6.3) Формула Рунге-Кутта 2го порядка с усреднением по

времени.