Замечание. Математическое ожидание полностью случайную величину не характеризует, так как можно найти различные случайные величины, имеющие одинаковые математические ожидания, но различные возможные значения. По этой причине вводят другие числовые характеристики, например, дисперсию, характеризующую рассеяние возможных значений случайной величины вокруг её математического ожидания.
Пусть Х – случайная величина, 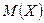 – её математическое ожидание. Тогда величина
– её математическое ожидание. Тогда величина 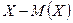 будет также случайной.
будет также случайной.
Определение 11. Отклонением случайной величины Х называют величину 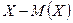 .
.
Замечание. При построении закона распределения вероятностей отклонения полагают, что вероятности отклонений совпадают с соответствующими вероятностями значений Х.
Теорема 1. Математическое ожидание отклонения равно нулю: 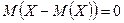 .
.
Доказательство. 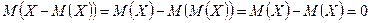 .
.
Определение 12. Дисперсией (рассеянием) 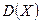 случайной величины называется математическое ожидание квадрата отклонения случайной величины от её математического ожидания:
случайной величины называется математическое ожидание квадрата отклонения случайной величины от её математического ожидания: 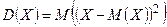 .
.
Замечание 1. Если дискретная случайная величина задана конечным рядом распределения, то её дисперсия вычисляется по формуле 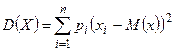 , вытекающей непосредственно из определений отклонения и дисперсии. Если дискретная случайная величина задана бесконечным рядом распределения, то дисперсия есть сумма ряда
, вытекающей непосредственно из определений отклонения и дисперсии. Если дискретная случайная величина задана бесконечным рядом распределения, то дисперсия есть сумма ряда 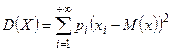 , при условии, что ряд сходится абсолютно.
, при условии, что ряд сходится абсолютно.
|
|
|
Замечание 2. Из определения следует, что дисперсия ДСВ есть неслучайная (постоянная) величина.
Теорема 2. Дисперсия равна разности между математическим ожиданием квадрата случайной величины Х и квадрата её математического ожидания: 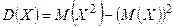 .
.
Доказательство. По свойствам математического ожидания имеем:
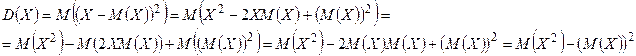
Замечание. В силу теоремы 2 дисперсию дискретной случайной величины, заданной конечным рядом распределения, можно вычислять по формуле 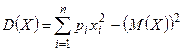 .
.
 2014-02-02
2014-02-02 960
960








