Потенциал электростатического поля. Связь потенциала

с напряжённостью электростатического поля

Как видно из уравнения (1.11), потенциальная энергия заряда q в поле заряда Q зависит от величины заряда q. Повторяя те же рассуждения, что и при выводе формулы (1.3) для напряжённости электрического поля, приходим к выводу, что отношение потенциальной энергии заряда в данной точке поля к величине заряда не зависит от величины этого заряда и может служить, таким образом, ещё одной характеристикой поля. Эта характеристика называется потенциалом

. (1.12)

Единица измерения потенциала – Вольт: 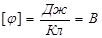. Поскольку на бесконечности потенциальная энергия взаимодействующих зарядов равна нулю, то и потенциал поля на бесконечности тоже равен нулю. Из выражения (1.12) следует определение потенциала – это есть потенциальная энергия единичного положительного заряда, помещённого в данную точку поля. Таким образом, потенциал – это энергетическая характеристика поля. Из сравнения формул (1.11) и (1.12) следует, что потенциал, создаваемый точечным зарядом в данной точке поля, определяется как

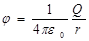. (1.13)

Из формул (1.6), (1.9) и (1.12) следует:

,

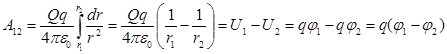или работа по перемещению точечного заряда между двумя точками в электростатическом поле равна произведению величины заряда на разность потенциалов между начальной и конечной точками:

. (1.14)

Учитывая, что работа может быть также записана при помощи напряжённости электрического поля

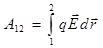, (1.15)

то из сравнения формул (1.14) и (1.15) получаем

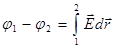. (1.16)

И напряжённость, и потенциал – это две характеристики одного и того же электростатического поля в данной точке. Следовательно, между ними должно быть некоторое соответствие, связь. Чтобы установить эту связь, рассмотрим работу по перемещению заряда вдоль оси х на расстояние dx, при этом разность потенциалов уменьшается на dj:

.

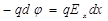Из последнего соотношения находим (сокращая на q)

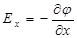. (1.17)

В формуле (1.17) введен символ частной производной ¶, чтобы подчеркнуть, что перемещение рассматривается только вдоль оси x. Аналогично находим и другие компоненты электрического поля 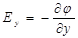и 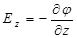. Из найденных компонент вектора 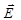можно составить весь вектор:

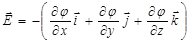. (1.18)

Здесь i, j, k – единичные векторы в направлении осей x, y,z. Выражение (1.18) можно сокращённо переписать, используя оператор “Ñ” – читается “набла”: 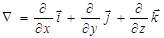. Поскольку в результате применения этого оператора к скалярной функции получаем вектор градиента этой функции, то

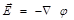, или . (1.19)

Чтобы сделать наглядным распределение потенциала, пользуются понятием эквипотенциальной поверхности – это поверхность, все точки которой обладают одинаковым потенциалом. Поскольку потенциал поля точечного заряда зависит только от расстояния до заряда (см. формулу (1.13)), то отсюда следует, что эквипотенциальными поверхностями для точечного заряда являются концентрические сферы. С другой стороны, линии напряжённости электрического поля направлены по радиусу от положительного заряда к отрицательному заряду. Таким образом, в случае точечного заряда линии напряжённости перпендикулярны к эквипотенциальным поверхностям. Можно, однако, показать, что этот вывод является общим – линии напряжённости всегда перпендикулярны к эквипотенциальным поверхностям.

1.5 Теорема Гаусса для напряжённости электростатического поля в интегральной и дифференциальной формах

Принцип суперпозиции (1.5), в принципе, позволяет рассчитать поле любой системы зарядов. Однако для задач, обладающих какой-либо симметрией, вычисление напряжённости значительно упрощается при помощи теоремы Гаусса. Прежде чем сформулируем эту теорему, введём понятие элементарного потока вектора напряжённости через произвольную площадку. Потоком вектора напряжённости через произвольную элементарную площадку dS называется скалярное произведение этого вектора на элемент поверхности .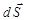

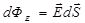. (1.20)

Теорема Гаусса гласит, что поток вектора напряжённости электростатического поля через любую замкнутую поверхность в вакууме равен алгебраической сумме зарядов, заключённых внутри этой поверхности, делённой на электрическую постоянную:

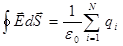. (1.21)

Для непрерывного распределения зарядов с некоторой объёмной плотностью 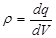, зависящей от координаты, 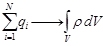, и вместо формулы (1.21) получаем:

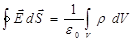. (1.22)

Гаусс получил формулу, которая связывает поток вектора через замкнутую поверхность с мощностью источника вектора (дивергенцией вектора) внутри этой поверхности 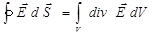, где дивергенция вектора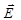

.

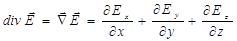Отсюда с учетом (1.22) следует

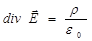. (1.23)

Последняя формула представляет собой теорему Гаусса для электростатического потенциала в вакууме в дифференциальной форме.