а) Поле бесконечно заряженной плоскости с поверхностной плотностью заряда s. Из соображений симметрии ясно, что поле будет направлено перпендикулярно плоскости – от плоскости для положительных зарядов, как показано на рис. 1.3, и к плоскости для отрицательных зарядов:
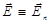 . (1.24)
. (1.24)
Кроме того, также из соображений симметрии ясно, что поле будет однородным. Представим цилиндрическую поверхность с образующими, перпендикулярными плоскости и с основанием DS. Посчитаем теперь поток через цилиндр. Поток через боковую поверхность равен нулю и, таким образом, весь поток через поверхность цилиндра сведётся к потоку через основания
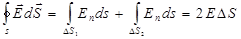 . (1.25)
. (1.25)
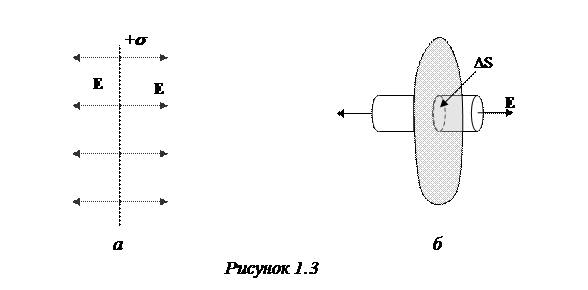
На основании теоремы Гаусса, этот поток равен заряду, заключённому внутри цилиндра, делённому на e0.
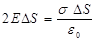 . (1.26),
. (1.26),
Откуда следует, что
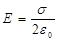 . (1.27)
. (1.27)
Таким образом, поле однородно заряженной плоскости:
- направлено перпендикулярно плоскости,
- является однородным,
- не зависит от расстояния до плоскости.
б) Поле 2-х разноименно заряженных плоскостей. Поле, образованное двумя разноименно заряженными плоскостями с поверхностной плотностью зарядов s, на основании принципа суперпозиции можно представить как наложение полей, созданных этими плоскостями отдельно. Поскольку эти поля в промежутке между плоскостями направлены одинаковым образом, то величина поля будет просто равна удвоенной величине поля, создаваемого одной плоскостью
|
|
|
 . (1.28)
. (1.28)
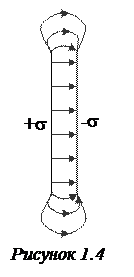 Вне объёма, ограниченного плоскостями, поля направлены в разные стороны, и результирующее поле равно нулю. Следовательно, поле, созданное двумя параллельными заряженными плоскостями:
Вне объёма, ограниченного плоскостями, поля направлены в разные стороны, и результирующее поле равно нулю. Следовательно, поле, созданное двумя параллельными заряженными плоскостями:
- является однородным,
- сосредоточено в промежутке между плоскостями.
Полученные выводы приближённо справедливы для плоских конденсаторов, для которых расстояние между плоскостями (их называют пластинами, или обкладками конденсатора) много меньше размеров пластин (рис. 1.4).
в) Поле бесконечного заряженного цилиндра. Пусть имеем бесконечный цилиндр радиуса R, заряженный с поверхностной плотностью заряда s (рис. 1.5). Из соображений симметрии ясно, что поле будет направлено перпендикулярно к оси цилиндра, и его величина будет зависеть от расстояния до цилиндра. Мысленно окружим наш цилиндр коаксиально расположенным цилиндром радиуса r и высотой h и посчитаем поток вектора напряжённости через поверхность, ограниченную этим цилиндром. Из соображений симметрии ясно, что поток через основания цилиндра будет равен нулю. Поток через боковую поверхность цилиндра будет равен E(r)2prh. На основании теоремы Гаусса он будет равен 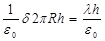 . Здесь l – линейная плотность заряда.
. Здесь l – линейная плотность заряда.
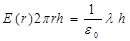 . (1.29)
. (1.29)
Откуда
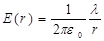 . (1.30)
. (1.30)
Выражение (1.30) справедливо для r>R. Внутри полого цилиндра, на основании теоремы Гаусса, поле равно нулю. Если мы составим цилиндрический конденсатор из двух коаксиальных заряженных цилиндров, то поле будет отличным от нуля только между цилиндрами, и его величина будет определяться выражением (1.30). Вне наружного цилиндра поле, на основании принципа суперпозиции, будет равно 0. Поле цилиндрического конденсатора (конечной длины) будет отличаться от поля цилиндрического конденсатора бесконечной длины только у краёв.
|
|
|
г) Поле заряженной сферической поверхности. Пусть есть сфера радиуса R, с плотностью поверхностного заряда s. Из соображений симметрии следует, что это поле будет центральным. Окружим нашу сферу другой концентрической сферой радиуса r. Если r>R, то на основании теоремы Гаусса
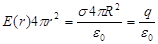 ,
,
откуда
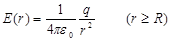 . (1.31)
. (1.31)
Внутри сферы поле равно нулю. Таким образом, поле равномерно заряженной сферы совпадает с полем точечного заряда, помещённого в центр сферы.
 2014-02-02
2014-02-02 6503
6503








