Моделирование многомерного нормального распределения

Средства моделирования статистических данных является незаменимыми инструментом для исследования возможностей применения того или иного статистического метода или разработки новой компьютерной технологии решения прикладных задач анализа данных.

Однако и в EXCEL и даже в таких известных пакетах по обработке статистических данных, как STATISTICA или SPSS представлены программные модули, позволяющие моделировать только одномерные статистические распределения.

Для моделирования многомерных данных обладающих свойствами реальных многомерных статистических данных нельзя использовать несколько раз процедуры моделирования одномерных данных, потому что в этом случае будут созданы независимые признаки и совместный анализ таких данных теряет смысл.

Для более адекватного отражения реальной ситуации при моделировании многомерных данных необходимо иметь возможность воспроизведения зависимости признаков. Среди многомерных законов распределения, учитывающих зависимость признаков наиболее известен многомерный нормальный закон. Плотность двумерного нормального распределения выражается формулой 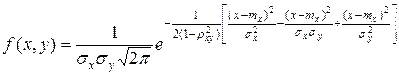(4.3):

(4.3)

Многомерная совместная нормальная функция плотности является обобщением двумерного случая. Для многомерной случайной величины 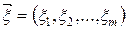многомерная нормальная плотность определяется по формуле(4.4):

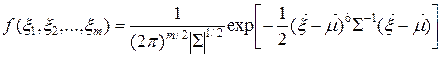, (4.4)

где 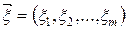- многомерная случайная величина, которая математически представляет собой вектор-столбец:

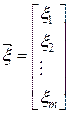(4.5)

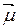- вектором математических ожиданий многомерной случайной величины :

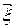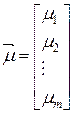(4.6)

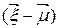- разность двух векторов дает вектор-столбец:

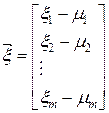(4.7)

В результате выполнения операции транспонирования получим вектор-строку

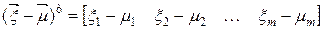(4.8)

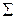- ковариационная матрица:

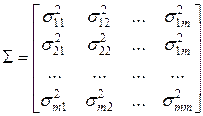, (4.9)

где 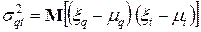q =1,2,3,… m, t =1,2,3,…, m;

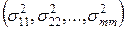- диагональные элементы представляют собой дисперсии признаков;

m – размерность многомерной случайной величины(количество признаков);

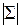- определитель ковариационной матрицы;

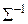- матрица обратная к ковариационной.

Мы разработали компьютерную программу моделирования многомерной нормальной выборки. В основу программы был положен алгоритм моделирования нормального распределения, изложенный в работе [S1]. Рассмотрим формальное описание алгоритма.

Вектор 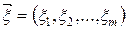произвольной нормально распределенной случайной величины можно получить специальным линейным преобразованием вектора 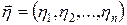, компоненты которого есть независимые нормально распределенные случайные величины с параметрами 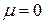,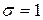. Для моделирования одномерной нормальной случайной величины существует множество способов. Самый простой способ моделирования состоит в преобразовании двух случайных чисел 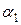и :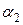

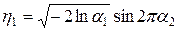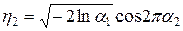, (4.10)

Преобразование 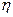в 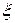производится по формуле:

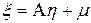(4.11)

В преобразовании участвует некоторая треугольная матрица A:

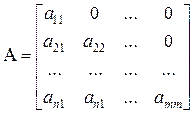(4.12)

Коэффициенты 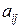могут быть определены с помощью рекуррентной процедуры. Общая рекуррентная формула имеет вид:

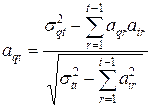(4.13)

где индексы изменяются в диапазоне 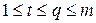, а суммы с верхним нулевым приделом равны нулю (, ).

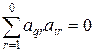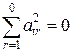Ключевым элементом алгоритма является вычисление матрицы преобразований A. Хотя алгоритм имеет строгое обоснование, общий вид расчетной формула для исследователей практиков носит характер справочной информации.

В простейших случаях моделирования двухмерных или даже трехмерных выборок выполнить расчеты матрицы преобразований может любой исследователь, занимающийся анализом многомерных данных. В двухмерном пространстве, формулы расчета элементов матрицы преобразования принимают достаточно простой вид:

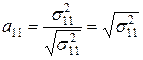(4.14)

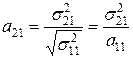(4.15)

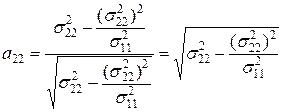(4.16)

Использование приведенных формул для моделирования двухмерного нормального закона мы можем продемонстрировать на примере решения задачи моделирования в EXCEL. Пусть задача состоит в моделировании трех классов нормальных выборок с заданными параметрами. Исходные данные задачи приведены на рис. 4.18.

Рис. 4.18. Исходные данные задачи

Первый шаг. На основании исходных данных рассчитаем корреляционные и ковариационные матрицы, а также матрицы преобразования по всем трем классам (рис. 4.19).

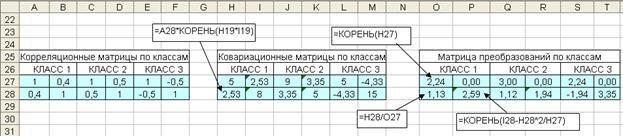
Рис. 4.19. Первый шаг алгоритма

Второй шаг. Для моделирования шести признаков (два признак – три класса) необходимо смоделировать шесть признаков стандартного нормального распределения n (0,1). Эти признаки обозначим 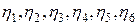(рис. 4.20). Для моделирования воспользуемся генератором случайных чисел “Пакета анализа”. Для расчета зависимых нормальных признаков X и Y по классам будем использовать матрицы преобразований (рис. 4.20).

По данным классифицированной модельной выборки, представленной в таблице данных, построим диаграмму рассеивания (рис 4.21). Изменяя исходные данные, задающие параметры классов на диаграмме рассеивания можно наблюдать изменения образов классов.

Рис. 4.20. Таблица модельных данных

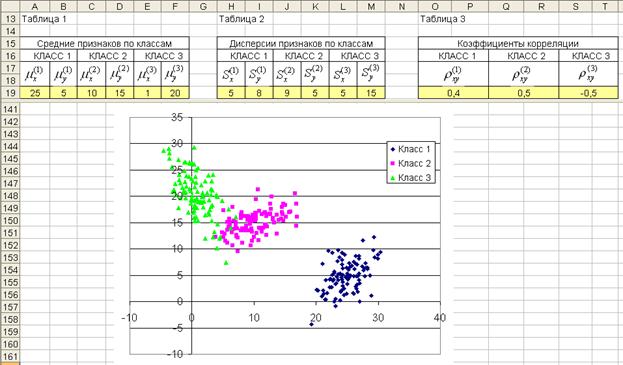
Рис. 4.21. Диаграмма рассеивания модельных данных

Таким образом, мы реализовали в EXCEL программу моделирующую смеси двухмерных нормальных распределений. Такие программы называются генераторами случайных чисел или симуляторами.

Для моделирования нормальных смесей с произвольным количеством классов мы разработали специальный программный модуль. Программный модуль был реализован в виде дополнительной надстройки к EXCEL, как самому распространенному среди практиков пакету по обработке данных. Тем более, что данные из пакета EXCEL без труда могут быть экспортированы в любой специализированный пакет по обработке статистических данных.

Программный модуль устанавливается в EXCEL после запуска специальной установочной программы. При установке программы необходимо установит низкий уровень безопасности (меню Сервис-Макрос-Безопасность). После установки программы на нижней панели EXCEL появится значок вызова программы моделирования

Рис. 4.22. Кнопка вызова программы моделирования нормальных смесей

Рассмотрим принцип работы программы. Для демонстрации программы будем использовать те же данные (три класса – два признака).

При моделировании данных, размерность которых свыше трех, необходимо задавать такие корреляционные матрицы, у которых ковариационная матрица положительно определена. В противном случае такие данные не могут быть смоделированы. Поэтому в процессе работы программы определяется это условие и выдается сообщение о его выполнении. Это условие следует из того, что зависимость двух признаков отражается и на зависимости их с третьим признаком.

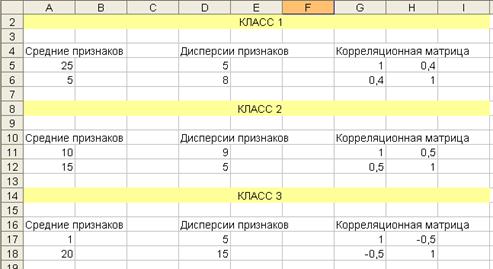
Рис. 4.23. Форма представления данных для моделирования трех классов

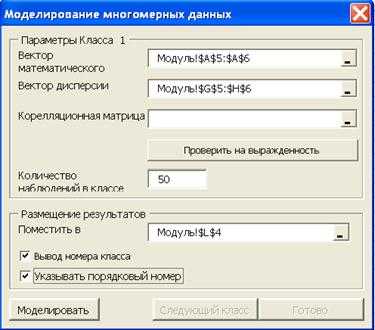
Рис. 4.24. Параметры программы моделирования нормальных смесей

Рассмотрим пример моделирования трех многомерных нормальных выборок с тремя зависимыми признаками. Совокупность объектов выборок составляют некоторые классы. При запуске программы для трех классов были установлены следующие объемы выборок 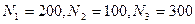. Остальные параметры многомерной выборки представлены в таб. 4.1. Различия в степени зависимости признаков задаются коэффициентами корреляционной матрицы. Как видно из таб.4.1, степень зависимости между признаками первого класса гораздо ниже, чем между признаками во втором и третьем классах. В силу того, что при моделировании используется датчик случайных чисел, параметры выборок, рассчитанные по модельным данным (таб.4.2), будут несколько отличаться от заданных параметров (таб. 4.1).

Таблица 4.1

Параметры, заданные при моделировании многомерной нормальной выборки

№ класса	Признак	Среднее	Дисперсия	Корреляционная матрица
Класс 1	Признак 1			1,0	0,3	0,2
Признак 2			0,3	1,0	0,1
Признак 3			0,2	0,1	1,0
Класс 2	Признак 1			1,0	0,5	0,5
Признак 2			0,5	1,0	0,5
Признак 3			0,5	0,5	1,0
Класс 3	Признак 1			1,0	0,9	0,8
Признак 2			0,9	1,0	0,9
Признак 3			0,8	0,9	1,0

Таблица 4.2

Параметры, рассчитанные по данным многомерной модельной выборки

№ класса	Признак	Среднее	Дисперсия	Корреляционная матрица
Класс 1	Признак 1	5,02	1,16	1,00	0,25	0,27
Признак 2	5,00	1,12	0,25	1,00	0,14
Признак 3	3,95	0,83	0,27	0,14	1,00
Класс 2	Признак 1	9,89	1,53	1,00	0,37	0,47
Признак 2	9,85	1,76	0,37	1,00	0,53
Признак 3	10,08	1,83	0,47	0,53	1,00
Класс 3	Признак 1	8,02	3,08	1,00	0,92	0,80
Признак 2	8,05	2,99	0,92	1,00	0,90
Признак 3	2,10	3,06	0,80	0,90	1,00

Приведем расчетные данные по матрице преобразований A для 1-го,2-го и 3-го классов.

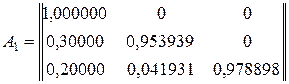(4.17)

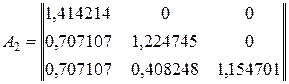(4.18)

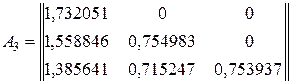(4.19)

Графический образ, сгенерированных данных можно проанализировать на трехмерном графике на рис. 4.25 и на трех двухмерных графиках, каких как на рис. 4.26.

Рис. 4.25. Трехмерная диаграмма рассеивания смоделированной многомерной выборки

Из диаграмм рассеивания многомерной выборки следует, что классы, визуально хорошо различимые в пространстве трех признаков. Различия классов проявляются и в проекции выборок на плоскость с осями “Признак 1” – “Признак 3” и в проекции на плоскость с осями “Признак 2” – “Признак 3”. Однако классы достаточно плохо визуально различимы на плоскости в координатах “Признак 1” – “Признак 2” (рис. 4.26).

Рис. 4.26. Проекция диаграммы рассеивания многомерной выборки на плоскость с осями “Признак 1” – “Признак 2”