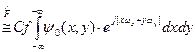Литература
М. Предко «Руководство по микроконтроллерам». Том 1. Москва: Постмаркет, 2001. – 416с.
Бродин В.Б., Шагурин И.И. «Микроконтроллеры. Архитектура, программирование, интерфейс». – М.: Издательство ЭКОМ, 1999. – 400с.
Atmel 8051-Architecture - Data Sheets AT89S8252 (31 pages, updated Dec 20 1997)
Домнин С.Б., Иванов Е.А., Муренко Л.Л. «Средства комплексной отладки микропроцессорных устройств».
М., "Энергоатомиздат", 1988.
Злобин В.К., Григорьев В. Л. «Программирование арифметических операций в микро-процессорах».
М., "Высшая школа", 1981.
Каган Б. М., Сташин В.В. «Основы проектирования микропроцессорных устройств автоматики».
М., "Энергоатомиздат", 1987
«Однокристальные микроЭВМ».
Справочник. М., "Микап", 1994.
Сташин В.В., Урусов А.В., Мологонцев О.Ф. «Проектирование цифровых устройств на однокристальных микроконтроллерах».
М., "Энергоатомиздат", 1990.
Інтернет. Сайт фірми Atmel https://www.atmel.com/
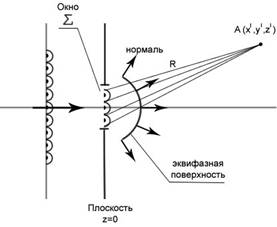
Рассмотрим падение световой волны на плоскость z=0 с окном Σ.
Каждая точка волнового фронта является источником сферической волны. Дальнейшее распространение волны определяется суммой сферических волн, проходящих в отверстие. При этом энергия передается не только в прямом направлении, но и в области геометрической тени.
Количественно: Нужно просуммировать волны, попавшие в окно Σ.
Поле в окне задано: 
Где 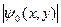 -амплитуда волны,
-амплитуда волны, 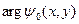 -фаза волны в каждой точке.
-фаза волны в каждой точке.
Рассчитаем поле в произвольной точке А пользуясь принципом Гюйгенса.
***
Плоская волна описывается уравнением 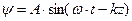 , знак – соответсвует волне, распространяющейся в направлении увеличения z, + - в противоположном направлении.
, знак – соответсвует волне, распространяющейся в направлении увеличения z, + - в противоположном направлении.
Экспоненциальная форма записи уравнения плоской волны: 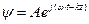
Такая форма записи удобна для дифференцирования в волновых уравнениях, но физический смысл имеет только мнимая часть этого выражения.
В теории дифракции, где учитывается монохроматичность волны (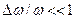 ), для удобства вычислений экспоненту
), для удобства вычислений экспоненту 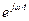 не пишут (но учитывают). Уравнение плоской волны записывают в виде:
не пишут (но учитывают). Уравнение плоской волны записывают в виде: 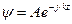
Сферическая волна Фаза волны меняется в пространстве, зависит от радиус-вектора r. Набег фазы определяется kr. Плотность потока энергии убывает обратно-пропорционально r2, а амплитуда убывает обратно-пропорционально r: 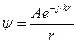
***
В точку А волна попадет, пройдя расстояние R, при этом надо учесть набег фаз.
В соответствии с принципом Гюйгенса поле в т.А равно:
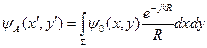
где интегрирование идет по всему окну, 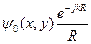 - вклад от одного элементарного источника, (x,y)-координаты точки в окне.
- вклад от одного элементарного источника, (x,y)-координаты точки в окне.
Расстояние: R=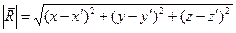 , подставляем в предыдущее уравнение:
, подставляем в предыдущее уравнение:

2. Рассмотрим задачу в параксиальном приближении.
Углы, под которыми видна т.А –малы. При этом  ,
, 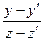 <<1. Рассмотрим корень
<<1. Рассмотрим корень  в параксиальном приближении.
в параксиальном приближении.
 =
= =
= т.к.
т.к. и z=0.
и z=0.
Выражение для  принимает вид:
принимает вид:

3. Выражение в знаменателе  можно заменить 1, т.к. в амплитуду выражение дает малые поправки, которыми можно пренебречь. В числителе в экспоненте мы не можем провести эту замену т.к. выражение оказывает существенное влияние на фазу. (Фаза определяется как
можно заменить 1, т.к. в амплитуду выражение дает малые поправки, которыми можно пренебречь. В числителе в экспоненте мы не можем провести эту замену т.к. выражение оказывает существенное влияние на фазу. (Фаза определяется как 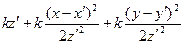 , где
, где 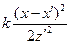 и
и  могут быть больше π)
могут быть больше π)
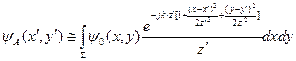

учитывая нормировочный множитель и множитель, постоянный по х и у:
 (переобозначение-
(переобозначение- =СФ)
=СФ)
Выражение описывает поле в произвольной точке А за экраном, оно определяет фундаментальное для физической оптики интегральное преобразование - преобразование Френеля 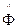 .
.

Рассмотрим уточнение преобразования Френеля.
4. Вынесем за знак интеграла множители, не содержащие переменных интегрирования:
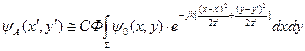 =
=
Переобозначим 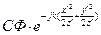 =Сf
=Сf
Приближение Релея: если  , то можно пренебречь фазой.
, то можно пренебречь фазой.
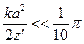 ,
,  ,
, 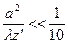 , где а –размер окна. Если точка очень далека от экрана, то с некоторого расстояния z’ условие начнет выполняться.
, где а –размер окна. Если точка очень далека от экрана, то с некоторого расстояния z’ условие начнет выполняться.
L- расстояние от окна до т. наблюдения, 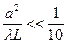 . Комбинация чисел
. Комбинация чисел  носит название число Френеля: Nфр=
носит название число Френеля: Nфр=
Рассматриваются такие области, где Nфр<<1, область пространства, где выполняется данное соотношение называется дальней зоной (зоной Фраунгофера)

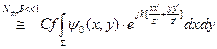 ,
, 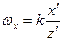 ,
,  (пространственная частота)
(пространственная частота)
***
 2014-02-03
2014-02-03 811
811