Сравнения и их свойства

Алгоритм Евклида нахождения наибольшего общего делителя

Пусть даны два натуральных числа a и b, a < b.

Найдем остатки от деления

b = a q₀ + r₁

a = r₁ q₁ + r₂

r₁ = r₂ q₂ + r₃

r₂ = r₃ q₃ + r₄

…………….

r_n-2 = r_n-1 q_n–1 + r_n

r_n-1 = r_n q_n

НОД(a, b) = r_n.

Пример. Найдем НОД(114, 534).

534 = 114*4 + 78, 114 = 78*1 + 36, 78 = 36*2 + 6, 36 = 6*6. НОД(114, 534)=6.

Возьмем натуральное число n и рассмотрим остатки от деления целых чисел на n.

Определение. Два целых a и b сравнимы по модулю n, если разность a – b делится на n без остатка:

a = b mod n (1)

Сравнения обладают следующими свойствами:

1. a = a mod n

2. a = b mod n Þ b = a mod n

3. a = b mod n и b = c mod n Þ a = c mod n

4. a = b mod n Þ k + b = k + a mod n

5. a = b mod n Þ k b = k a mod n

6. k b = k a mod n и (k, n) = 1 Þ a = b mod n

7. a = b mod n и c = d mod n Þ a + c = b + d mod n

8. a = b mod n и c = d mod n Þ a c = b d mod n

9. a = b mod n Þ a ^k = b ^k mod n для любого целого k

10. a = b mod n Þ a = b + n t, где t – целое число

Запись 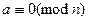означает, что само число a делится на 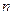, т.е. .

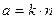Если зафиксировать некоторый модуль сравнения 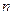, то всякое натуральное число 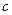можно единственным образом представить в виде

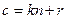, (2)

где 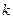– частное от деления н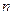а , а 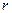– остаток, совпадающий с одним из чисел

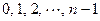
Остаток 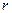называют вычетом числа 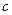по модулю 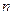. Запись вида (2), где 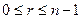, допускает не только натуральные, но и любые целые числа. Из равенства (2) следует, что 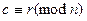, т.е. всякое число сравнимо со своим остатком (вычетом) по модулю .

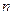Пусть 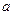и 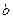– два произвольных числа, записанные в виде (2):

, .

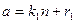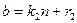Каждый из остатков 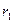и 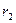– это одно из чисел множества {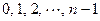}, поэтому их разность может делиться на 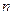лишь в одном случае, когда 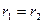. Но тогда и разность 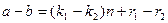может делиться на 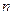тогда и только тогда, когда 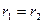. Отсюда следует, что 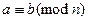тогда и только тогда, когда числа 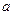и 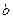имеют одинаковые остатки при делении на .

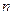Определение. Классом вычетов 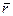по модулю 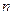называются все числа, имеющие один и тот же вычет 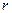по модулю 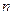, и, следовательно, сравнимые между собой по этому модулю:

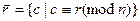
Каждому вычету 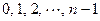отвечает свой класс вычетов: .

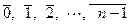Классы вычетов попарно не пересекаются, и каждое целое число попадает ровно в один класс. Используя операции сложения и умножения чисел, можно производить аналогичные операции и над классами вычетов.

Пусть 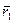и 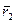– два класса вычетов. Выберем любые два числа из этих классов: 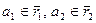. Пусть оказалось, что сумма 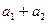имеет вычет 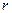, а произведение 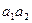– вычет :

.

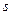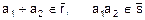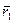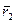Тогда будем считать, что «сумма» классов и равна 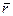, а их «произведение» равно :

.

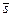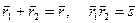Класс, которому принадлежит сумма 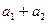(соответственно произведение 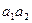) не зависит от выбора элементов 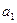и 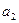в классах 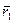и .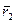

Пример. Пусть модуль сравнения 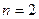. В этом случае имеем два класса вычетов – 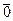и 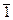, а операции над ними выглядят так:

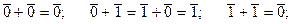
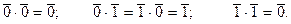
Часто в обозначениях классов вычетов опускают черту, записывая их как обычные натуральные числа.

Функция Эйлера [1]

Определение. Функцией Эйлера j(n) называется число натуральных чисел, не превосходящих n и взаимно простых с n.

Утверждение. Если a, b – взаимно просты, (a, b) = 1, то j( a b ) = j( a ) j( b ).

Утверждение. Если p – простое число, то j( p ^a ) = p ^{a – 1} (p – 1).

Утверждение. Если p – простое число, то j( p ) = p – 1.

Утверждение. Если 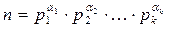, где p ₁, p ₂,…, p _k – попарно различные простые числа, то 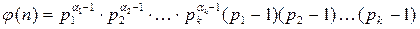или

.

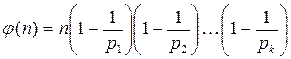Пример. j( 45 ) = j( 9 ) j( 5 ) = 3*2*4 = 24.

Утверджение (теорема Эйлера). Если a и n взаимно просты, то a ^{j ( n )}= 1 mod n.

Утверджение (малая теорема Ферма). Если p – простое число и a < p., то a ^{p – 1} = 1 mod p.

Контрольные вопросы

1. Дайте определение взаимно простых чисел.

2. Определите НОД и НОК.

3. Опишите алгоритм Евклида нахождения НОД.

4. Что означает, что два числа сравнимы по модулю.

5. Каковы свойства сравнений.

6. Что такое классы вычетов?

7. Определите функцию Эйлера.

8. По каким формулам можно вычислять функцию Эйлера?

9. Сформулируйте теорему Эйлера.

10. Сформулируйте малую теорему Ферма.

11. В каких криптографических алгоритмах используются сравнения?