1) Если 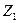 µ
µ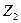 , то
, то 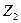 Î Р Þ
Î Р Þ 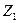 Î Р;
Î Р;
2) Если 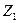 µ
µ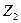 и
и 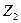 µ
µ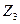 , то
, то 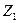 µ
µ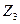 ;
;
3) Если 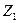 Î NР,
Î NР, 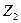 Î NР,
Î NР, 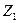 Î NРС и
Î NРС и 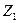 µ
µ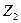 , то
, то 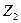 Î NРС. Доказательство вытекает из определений 2.1, 3.1, 4.1 и 4.2.
Î NРС. Доказательство вытекает из определений 2.1, 3.1, 4.1 и 4.2.
Теорема 4.1 указывает способ доказательства. NР -полноты некоторой задачи Z, если известна хотя он одна NР -полная задача Z*: достаточно доказать, что 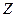 Î NР и что Z*µ Z.
Î NР и что Z*µ Z.
Если предположить, что классы P и NP совпадают, что означает существование полиномиального алгоритма решения любой задачи из NP, то это повлекло бы существование полиномиальных алгоритмов решения всех NР -полных задач. Однако за всю историю развития математики не было найдено ни одного полиномиального алгоритма решения хотя бы одной какой-нибудь известной NР -полной задачи. Это послужило обоснованием существующей на сегодняшний день научной гипотезы
P ≠ NP
На рис.4.2 приведена теоретико-множественная диаграмма класса NP в предположении, что P ¹ NP.
Литература:
1. Гэри М., Джонсон Д. Вычислительные машины и труднорешаемые задачи. М.: Мир, 1982. – 416 с.
2. Ахо А., Хопкрофт Д., Ульман Д. Построение и анализ вычислительных алгоритмов. М.: Мир, 1979. – 536 с.
3. Грэхем Р., Кнут Д., Паташник О. Конкретная математика (основание информатики). М.: Мир, 1998. – 703 с.
4. Донской В. И. Дискретная математика. –Симферополь: Сонат, 2000. –356 с.
5. Липский В. Комбинаторика для программистов. М.: Мир, 1988. – 215 с.
6. Лавров И. А., Максимова Л. Л. Задачи по теории множеств, математической логике и теории алгоритмов. М.: Физико-математическая литература, 1995. – 256 с
7. Линдон Р. Заметки по логике. М.: Мир, 1968. – 128 с.
8. Оре О. Теория графов. М.: Наука, 1980. – 336 с.
9. Шоломов Л. А. Основы теории дискретных логических и вычислительных устройств. М.: Наука, 1980. – 400 с.
 2014-02-13
2014-02-13 466
466








