Расчет теоретических частот

Решение

Для расчета теоретических частот вычислим нормированные величины u_i; u_i+1:

1 интервал: -∞; ;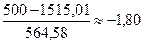

2 интервал: -1,80; ;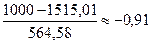

3 интервал: -0,91; ;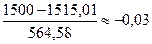

4 интервал: -0,03; ;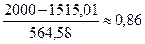

5 интервал: 0,86; ;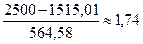

6 интервал: 1,74; ∞.

Таблица 7

№	Границы интервалов хi; хi+1	Границы интервалов ui; ui+1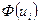
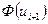
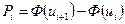
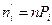
	-∞; 500	-∞; -1,80		0,0360	0,0360	28,18
	500; 1000	-1,80; -0,91	0,0360	0,1814	0,1454	113,85
	1000; 1500	-0,91; -0,03	0,1814	0,4881	0,3067	240,15
	1500; 2000	-0,03; 0,86	0,4881	0,8051	0,3170	248,21
	2000; 2500	0,86; 1,74	0,8051	0,9591	0,1540	120,58
	2500; ∞	1,74; ∞	0,9591		0,0409	32,02
	Итого	-	-	-

Наглядно расхождение эмпирических и теоретических частот можно показать с помощью полигона (рис. 3).

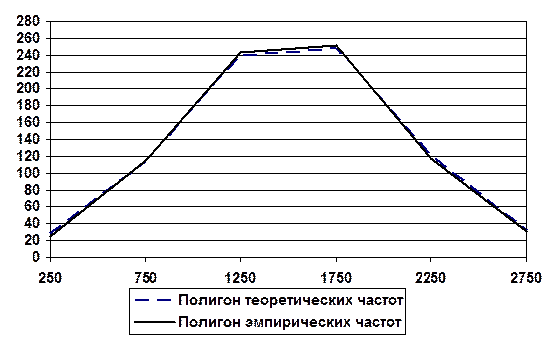
Рисунок 2. Полигон теоретических и эмпирических частот

3 этап: проверка гипотезы о законе распределения.

Как бы хорошо ни был подобран теоретический закон распределения, между эмпирическим и теоретическим распределениями неизбежны расхождения. Закономерно возникает вопрос: объясняются ли эти расхождения только случайными обстоятельствами, связанными с ограниченным числом наблюдений, или они являются существенными и связаны с тем, теоретический закон распределения подобран неудачно. Для ответа на данный вопрос служат критерии согласия.

Пусть необходимо проверить нулевую гипотезу H₀ о том, что исследуемая случайная величина X подчиняется определенному закону распределения. Для проверки гипотезы H₀ выбирают некоторую случайную величину U, характеризующую степень расхождения теоретического и эмпирического распределений, закон распределения которой при достаточно больших n известен и практически не зависит от закона распределения случайной величины X.

Зная закон распределения U, можно найти вероятность того, что U приняла значение не меньше, чем фактически наблюдаемое в опыте u, т.е. 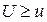. Если 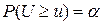мала, то это означает в соответствии с принципом практической уверенности, что такие как в опыте, и бóльшие отклонения практически невозможны. В этом случае гипотезу H₀ отвергают. Если же вероятность 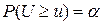не мала, расхождение между эмпирическим и теоретическим распределениями несущественно и гипотезу H₀ можно считать не противоречащей опытным данным.

Наиболее часто в практике статистических исследований используются критерии согласия К. Пирсона (хи-квадрат), В.И. Романовского, А.Н. Колмогорова, Б.С. Ястремского.

В χ²-критерий Пирсона в качестве меры расхождения U берется величина χ², равная:

,

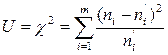которая имеет χ²-распределение с 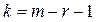степенями свободы, где m – число интервалов эмпирического распределения (вариационного ряда); r – число параметров теоретического распределения.

Схема применения χ²-критерия для проверки гипотезы H₀ сводится к следующему:

1) определяется мера расхождения эмпирических и теоретических часто χ²;

2) для заданного уровня значимости α (как правило, принимается на уровне 0,05 или 0,01) по справочной таблице χ²-распределения находят критическое значение 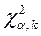при числе степеней свободы ;

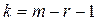3) если расчетное значение χ² больше критического 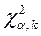, т.е. 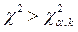, то гипотеза H₀ отвергается, если 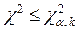, то гипотеза H₀ не противоречит опытным данным.

Примечание: статистика χ² имеет χ²-распределение лишь при 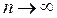, поэтому необходимо, чтобы в каждом интервале было достаточное количество наблюдений, по крайней мере, не меньше 5. Если какой-либо интервал не удовлетворяет данному требованию, то имеет смысл объединить его с соседним таким образом, чтобы в объединенных интервалах 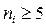. В данном случае параметр m при расчете числа степеней свободы уменьшается на число таких объединенных интервалов.

На практике кроме критерия χ² часто используют критерий Колмогорова, в котором в качестве меры расхождения между теоретическим и эмпирическим распределениями рассматривают максимальное значение абсолютной величины разности между эмпирической и теоретической функциями распределения:

,

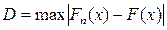называемое статистикой критерия Колмогорова.

Схема применения критерия Колмогорова:

1) строятся эмпирическая функция распределения и предполагаемая теоретическая;

2) определяется мера расхождения между теоретическим и эмпирическим распределением D и вычисляется величина:

;

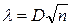3) если вычисленное значение λ окажется не больше критического λ_α, определенного на уровне значимости α (λ_0,05 =1,36; λ_0,01 =1,63), то нулевая гипотеза H₀ не противоречит опытным данным.

Примечание: применение критерия Колмогорова в принципе возможно лишь тогда, когда теоретическая функция распределения задана полностью. Однако такие случаи в практике встречаются редко. Обычно из теоретических соображений известен лишь вид функции распределения, а ее параметры определяются по эмпирическим данным. При применении критерия χ² это обстоятельство учитывается соответствующим уменьшением числа степеней свободы. Такого рода поправок в критерии Колмогорова не предусмотрено. Поэтому, если при неизвестных значениях параметров применить критерий Колмогорова, взяв за значения параметров их оценки, вычисленные по выборке, то получим завышенное значение вероятности 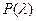, и, следовательно, бóльшее критическое значение λ_α. В результате есть риск в ряде случаев принять нулевую гипотезу H₀ о законе распределения случайной величины как правдоподобную, в то время как на самом деле она противоречит опытным данным.

Пример 7.7. По данным примеров 7.3 и 7.5 на уровне значимости α=0,05 проверить гипотезу H₀ о том, что случайная величина Х – число поврежденных изделий, распределена по закону Пуассона.

Для определения статистики χ² составим таблицу: