Разработка схем активных фильтров по заданным требованиям к их ЛАЧХ

Исходные данные для проектирования фильтра содержат требования к частотной характеристике в области полосы пропускания и в переходной области от полосы пропускания к полосе задерживания. Так, для полосы пропускания задаются ее границы и максимально допустимое отклонение модуля коэффициента передачи сигнала от заданного значения, выраженное в децибелах и обозначаемое 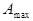, для переходной области задается минимально допустимое затухание на заданной частоте 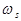выраженное также в децибелах и обозначаемое .

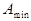Для реализации частотной характеристики, удовлетворяющей заданным требованиям, необходимо решить задачу выбора подходящей функции или .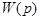

В общем виде для 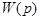можно записать

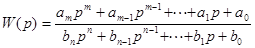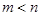, где (1)

Полиномы числителя и знаменателя можно разложить на множители и записать

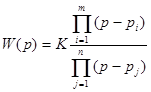, (2)

где и 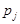- нули и полюсы комплексной функции .

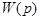При 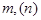четном все нули (полюсы) образуют комплексно-сопряженные пары, при этом

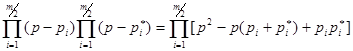, (3)

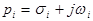где , а .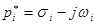

При 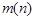нечетном получим

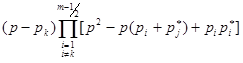. (4)

Таким образом, в общем случае, например, для фильтра нижних частот передаточная функция представляется в виде

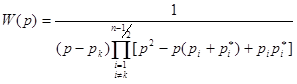, (5)

а соответствующая структурная схема представляет собой каскадное соединение 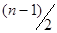звеньев второго порядка и одного звена 1-ого порядка.

При решении задачи аппроксимации заданной частотной характеристики определяют порядок фильтра, т.е. величину 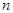, значения постоянных коэффициентов таким образом, чтобы обеспечить выполнение заданных требований и получить аналитическое выражение для аппроксимирующей функции, например, ФНЧ в виде (5). Это оказывается возможным при использовании для целей аппроксимации полиномов Баттерворта и Чебышева, отличительной особенностью которых является то, что они дают возможность аналитического определения значений корней при любом порядке полинома.

Полином Баттерворта имеет вид

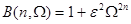, (6)

при его использовании для аппроксимации квадрата модуля частотной характеристики ФНЧ получаем

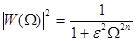, (7)

где - некоторая нормированная (безразмерная) частота. При использовании логарифмического масштаба (7) определяется как 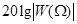. На Рис.1 представлены графики соответствующих частотных характеристик для различных значений 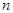и шага кратности по 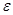, обозначенного через .

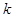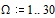
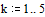
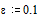
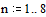
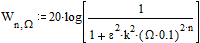
Рис.1. Семейство графиков нормированных логарифмических частотных характеристик ФНЧ Баттерворта.

Связь задаваемых для ФНЧ параметров с коэффициентам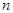и и 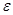определяется следующим образом: величина отклонения логарифмической частотной характеристики от максимального уровня ноль децибелл на частоте соответствует частоте 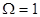и равно

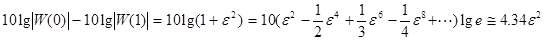[дб]

При использовании линейного масштаба величина отклонения квадрата модуля ЧХ на этой же частоте равна .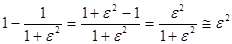

При заданной величине максимально допустимого отклонения логарифмической частотной характеристики (ЛЧХ) на нормированной частоте 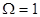величина 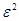может быть определена из уравнения 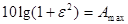, откуда получаем

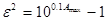(8)

При заданном минимально допустимом затухании на частоте 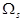, аналогично составляем уравнение 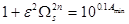, подставляя в которое уже найденное значение 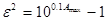и решая его относительно 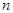получаем

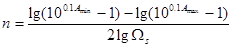(9)

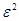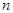При известных значениях и полином Баттерворта может быть представлен в виде произведений квадратных трехчленов и двучленов с известными коэффициентами, которые приводятся в соответствующих таблицах.

Полином Чебышева имеет вид

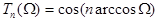, (10)

при его использовании для аппроксимации квадрата модуля частотной характеристики ФНЧ получаем

(11)

Полиномиальная форма (10) может быть получена на основе следующих рекурентных соотношений

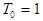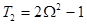, , ,... . (12)

На Рис.2 приведены графики ЛЧХ ФНЧ Чебышева для различных 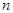и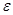

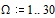
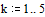
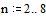
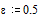
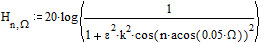
Рис.2. Семейство графиков нормированных логарифмических частотных характеристик ФНЧ Чебышева

Как видно, отличительной особенностью фильтров Чебышева является волнообразный характер частотной характеристики в пределах полосы пропускания.

При выборе аппроксимации заданной частотной характеристики по Чебышеву необходимый порядок фильтра определяется по формуле

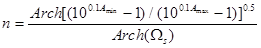(13)

Вычисление корней полиномов Баттерворта.

Корни полинома Баттерворта определяются в результате решения уравнения вида:

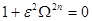. Введем комплексную переменную 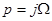, тогда 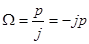и исходное уравнение принимает вид: . Из этого уравнения получаем:

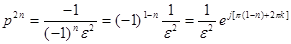, откуда формула для вычисления k-ого корня полинома порядка n определяется в виде 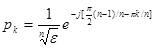. Так, для n=2 получаем

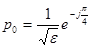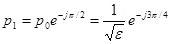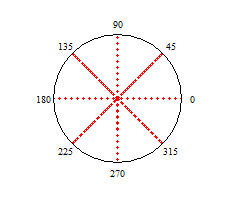
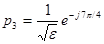, , , . Расположению корней на комплексной плоскости соответствует следующая круговая диаграмма. Ось мнимых чисел на диаграмме направлена вертикально, а ось вещественных чисел горизонтально. Из диаграммы видно, что пары корне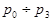й и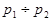

являются комплексно-сопряженными, им соответствуют аргументы 45 градусов, 315 градусов и 225 градусов, 135 градусов, соответственно.

При известных значениях корней исходный полином представляется в виде

.

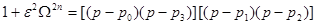Для первой и второй квадратных скобок соответственно получаем:

,

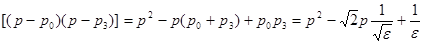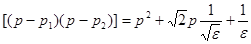, таким образом, квадрат модуля полинома Баттерворта второго порядка представляется в виде произведения комплексно-сопряженных множителей второго порядка, каждому из которых может быть сопоставлена одна из ранее рассмотренных схем активных фильтров второго порядка. На этом основан метод проектирования схемы по заданным требованиям к частотной характеристике.

Вычисление корней полинома Чебышева.

Корни полиномов Чебышева определяются в результате решения уравнения вида

. Приведем это уравнение к виду

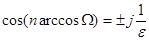и для решения используем подстановку

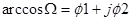, тогда 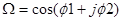. Далее определим

.

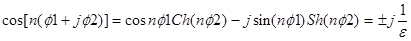C учетом того, что в правой части мнимое число, можем вещественное слагаемое левой части приравнять нулю: 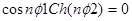, откуда , , 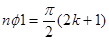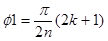. Из равенства мнимых частей слева и справа получим:

, откуда . Окончательно для k-ого корня получаем в общем виде формулу: .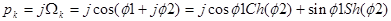

Формулы для полиномов Баттерворта и Чебышева в виде произведения сомножителей второго и первого порядка приводятся в литературе по проектированию фильтров, см., например, Мошиц Г., Хорн П. Проектирование активных фильтров. М.:Мир, 1984.

Методика разработки схем изложена в методическом пособии “ Применение интегральных микросхем операционных усилителей в схемах активных RC-фильтров и стабилизированных RC-генераторов”, автор Кавокин В.П., издание СПбГМТУ, 1997.