Основные теоремы о непрерывных функциях

Классификация точек разрыва функции.

Определение: Пусть y=f(x) определена в О°(х₀), а в самой точке х₀ может быть как и определена, так и неопределенна.

1) Точка х₀ называется точкой разрыва 1 ^ого рода функции, если

а) Существует lim f(x)’=lim f(x)’’, но либо функция неопределенна в точки х₀ либо f(x₀)¹b. Тогда точка х₀

^x®x_°^{+0 x®x}_°^-0

точка устранимого разрыва.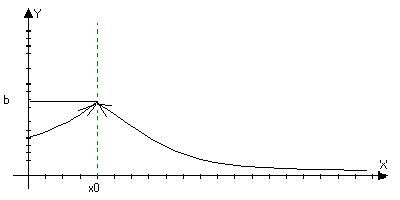

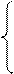1,x=1

Y=(x-1)/(x-1)=

Не $, x=1

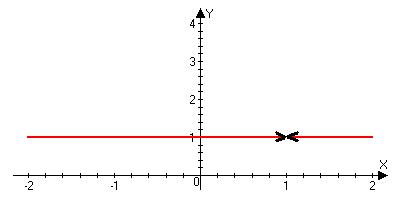
б) f(x)=c¹b

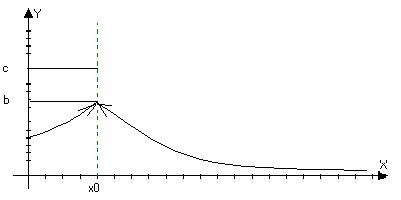
Можно доопределить или переопределить в точке х₀, так что она станет непрерывной.

$ lim f(x)=b; lim f(x)=c, но b¹c

^x®x_°^{+0 x®x}_°^-0

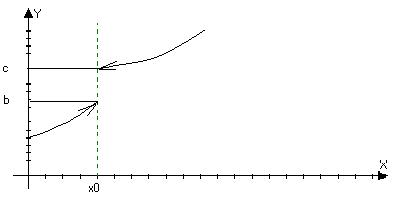
Может быть и определена f(x₀)=b

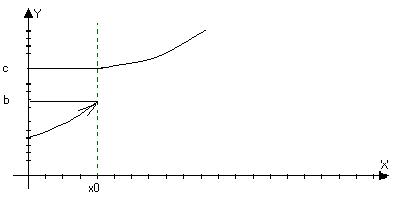
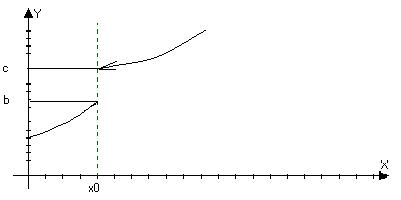
Или f(x₀)=d

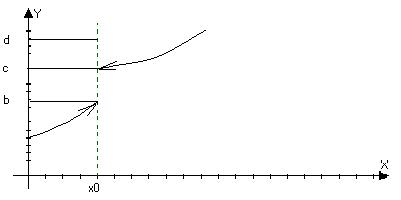
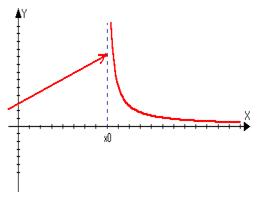2)Точка х₀ называется точкой разрыва 2 ^ого рода функции если она не является точкой разрыва 1 ^ого порядка, то есть если хотя бы один из односторонних пределов не существует или равен бесконечности.

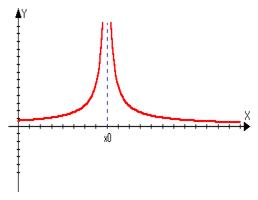
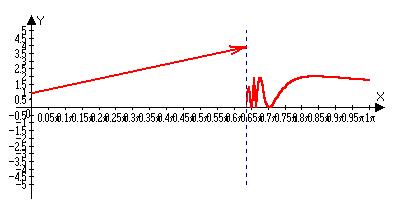
y=sin(1/x)

Теорема: Все основные элементы функции непрерывны в любой точки своей области определения.

Определение: (функции непрерывной на отрезке)

y=f(x) – называется непрерывной на отрезке [a,b], если она непрерывна в любой точке хÎ(a,b). В точке х=а функция непрерывна справа, то есть lim f(x)=f(a), а в точке х=b функция непрерывна слева lim f(x)=f(b).

^x®x_°^{+0 x®x}_°^-0

Функция непрерывна на множестве D если она непрерывна в этой точке.

Теорема: (о сохранение знака непрерывной функции)

Пусть y=f(x) непрерывна в точке х₀ и f(x₀)>0 (f(x₀)<0), тогда f(x)>0 f(x)<0 непрерывна в некоторой точки О(х₀)

Доказательство: $ lim f(x)=f(x₀)Û "ε>0 $ d>0 "x: |x-x₀|<d Þ |f(x)-f(x₀)|<ε.

^x®x_°

Пусть f(x₀)>0, выберем ε=f(x₀) Þ |f(x)-f(x₀)|<f(x₀) "xÎO_d(x₀) ($d>0!)

-f(x₀)<f(x)-f(x₀)<f(x₀); f(x)>0 "xÎO_d(x₀), если f(x₀)<0, то ε=-f(x₀)

Теорема Коши: (о нуле непрерывной функции)

Пусть f(x) непрерывна на [a,b] и на концах его принимает значение разных знаков f(a) f(b) <0, тогда $ x₀Î(a,b): f(x₀)=0

Доказательство:

f(b)>0 f(a)<0

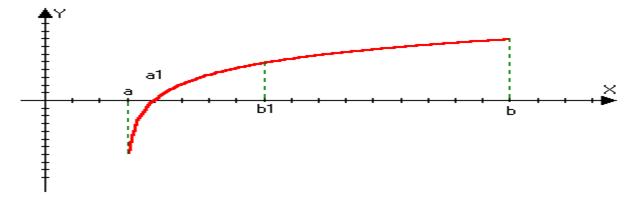
Разделим отрезок [a,b] пополам. Если в середине отрезка f(x)=0, то всё доказано, если нет, то выберем ту половину отрезка, на концах которой функция принимает значение разных знаков. Выбранной отрезок поделим пополам. Если в середине нового отрезка f(x)=0, то всё доказано, если нет, то выберем ту половину от той половины, на концах которой функция принимает значение разных знаков и т.д.

[a,b]É[a₁,b₁]É[a₂,b₂]

Последовательность левых концов удовлетворяет отношению a<a₁<a₂<…<a_n<…<b

b³b₁³b₂³…³b_n³…>a Þ

{a_n}-ограниченная не убывающая $ lim a_n=a£b f(a)<0 f(a_n)<0 "n

^x®+¥ |[a_nb_n]|=(b-a)/2ⁿ ®0 при n®¥

{b_n}-ограниченная не возрастающая $ lim b_n=b³a f(b)>0 f(b_n)>0 "n

^x®+¥

В силу непрерывности функции lim f(a_n)=f (lim b_n)=f(b)³0 lim (b_n-a_n)=b-a= lim (b-a)/2ⁿ=0Þa=b

^{x®+¥ x®+¥ x®+¥ x®+¥}

f(a)£0

Þ f(a)=0 x₀=a

f(b)=f(a)³0

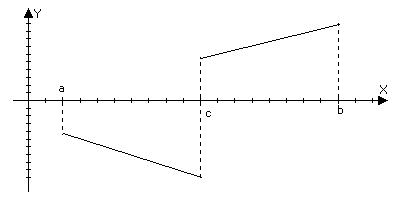
Условие непрерывности функции нельзя отбросить: f(b)>0; f(a)<0

Теоремы Вейштрасса.

1) Теорема: Пусть функция y=f(x) непрерывна на отрезке [a,b]. Тогда она ограниченна на нём.

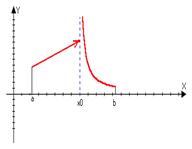Замечание: а) Условие непрерывности нельзя отбросить

Неограниченна сверху Þ неограниченна

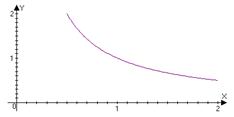б) Нельзя заменить отрезок на интервал или

полуинтервал.

Непрерывна на (0;1]

2) Теорема: Пусть функция y=f(x) непрерывна на отрезке [a,b]. Среди её значений есть наибольшее и наименьшее.

Замечание: а) Множество [0;1] наибольшее значение 1ÎМ

наименьшее значение 0 Î М

б) Множество (0;1]=М наибольшее значение 1ÎМ

нет наименьшего

в) Множество [0;1)=M нет наибольшего

наименьшее значение 0 Î М

г) Множество (0;1)=М нет ни того не другого.

Условие отрезка нельзя заменить на интервал или полуинтервал.

xÎ(0;1] непрерывна на (0;1] нет наибольшего значения