Основные теоремы о производной

Геометрический смысл производной.

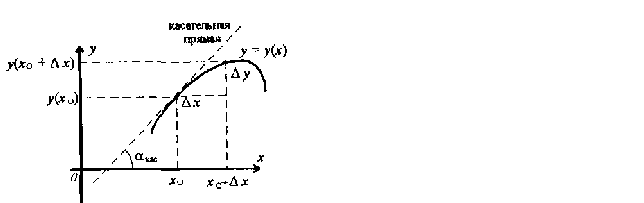y’(x₀)=lim∆y/∆x – производная функции у(х) и в точке х₀.

^∆х®0

∆y=y(x₀+∆x)-y(x₀)

y’(x₀)=tga_кас где a_кас – угол наклона в точке (х₀;y(x₀)) к оси

Теорема: Пусть $ f’(x) и g’(x), тогда $ [f(x)+g(x)]’= f’(x)+g’(x)

Доказательство: следует непосредственно из определения производной и свойств предела суммы.

Теорема: (связи между непрерывностью функции и существование производной)

Пусть $ f’(x)Þ функция f(x) – непрерывна.

Доказательство: Пусть f(x) определена в О(х₀) и lim[f(x)-f(x₀)]/(x-x₀)=f’(x₀)<¥Þ [f(x)-f(x₀)]/(x-x₀)=f(x₀)+a(x-x₀)[2]

^∆x®x_°

[f(x)-f(x₀)]=f’(x₀)(x-x₀)+a(x-x₀)(x-x₀) при х®х₀

lin[f(x)-f(x₀)]=limf’(x₀)(x-x₀)+lima(x-x₀)(x-x₀)=0+0=0Þlinf(x)=f(x₀) то есть f(x) непрерывна в точки х₀

^x®x_° ^x®x_° ^x®x_° ^x®x_°

Замечание: обратное утверждение неверно, из-за непрерывности функции в точке х₀ не следует существование функции в этой точки.

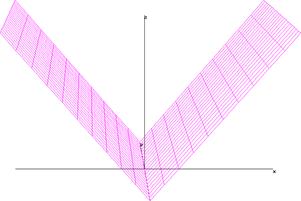y=|х

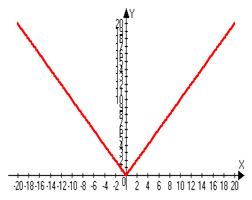
Непрерывна в точки х₀=0

limx, x³0

^x®+0

lim|x|= =0

lim(-x), x<0

^x®-0

y(0)=0

limy(x)=limy(x)=y(0)=0 Û $ limy(x)=y(0)=0 Þ функция непрерывна

^{x®+0 x®-0 x®0}

lim∆y/∆x-не существует, действительно х®+0Þy(x)=x

^x®0

lim[y(x)-y(0)]/x=lim(x-0)/x=1

^{x®+0 x®+0}

x®-0Þy(x)=-x

lim[y(0)-y(x)]/x=lim(0-x)/x=-1 то есть lim∆y/∆x – не существует

^{x®-0 x®-0 х®0}

Теорема: Пусть $ u’(x) и v’(x), тогда $(uv)’=u’v+v’u

Доказательство: Зададим приращение ∆х в точки х. Рассмотрим: lim[∆(uv)]/∆x=

^∆x®0

lim[1/∆x][u(x+∆x)v(x+∆x)-u(x)v(x)]=lim[1/∆x][ u(x+∆x)v(x+∆x)-u(x)v(x+∆x)+u(x)v(x+∆x)-u(x)v(x)=

^{∆x®0 ∆x®0}

lim[(v(x+∆x))(u(x+∆x)-u(x))]/∆x+lim[(u(x))(v(x+∆x)-v(x))]/∆x=v(x)u’(x)+u(x)v’(x)

^{∆x®0 ∆x®0}

Теорема: (о произведение частного)

Пусть $ u’(x) и v’(x), v’(x)¹0 в О(х), тогда $(u/v)’=[u’v-v’u]/v²

Доказательство: (u/v)’=[u(1/v)]’=[u’(1/v)]+[(1/v)’u]. Функция u(x) и v(x) –непрерывны в точки х₀.

lim[∆(1/v)/∆x]=lim[1/∆x][1/(v(x+∆x))-1/v(x)]=lim[[v(x)-v(x-∆x)]/[∆xv(x)x(x+∆x)]]-[v’(x)/v²(x)]

^{∆x®0 ∆x®0 ∆x®0}

(u/v)’=u’(1/v)-(uv)’/v²=[u’v-uv’]/v² что и требовалось доказать