Этапы минимизации ДНФ

В силу теоремы 6 получение минимальной ДНФ мож­но разбить на два этапа

1. Нахождение сокращенной ДНФ.

2. Нахождение тупиковых ДНФ (таких, из которых нельзя уда­лить ни одного простого импликанта) путём удаления подмно­жества элементарных конъюнкций из сокращённой ДНФ. Вы­бор минимальной из полученных тупиковых ДНФ.

Рассмотрим первый этап получения минимальной ДНФ. Ме­тод получения сокращённой ДНФ функции f(x₁,..., x_n) из ее совер­шенной ДНФ состоит в применении следующих эквивалентных преобразо­ваний:

а) операции полного склеивания, которая состоит в замене выражения А х Ú А`х на А, так как

А х Ú А`х º А (х Ú`х) º A • 1 º A;

б) операции неполного склеивания, которая состоит в замене А х Ú А`х на А х Ú А`х Ú А, так как

А х Ú А`х Ú А º А (х Ú`х) Ú А º А • 1Ú A = A;

в) операции поглощения, которая состоит в замене АВ Ú А на А, так как

АВ Ú А º А (В Ú 1) º А.

Здесь А и В – произвольные элементарные конъ­юнк­ции.

Теорема 7 (без доказательства). Сокращённую ДНФ функ­ции f(x₁,..., x_n) можно получить из ее совершенной ДНФ, применяя все возможные операции неполного склеивания, а затем операции поглощения.

Пример 1. Построить сокращённую ДНФ функции
f(x₁, x₂) = x₁ ® х₂ из ее СДНФ:

f(x₁, x₂) =`х<sub>1</sub>`х₂ Ú`х<sub>1</sub> х<sub>2</sub> Ú х<sub>1</sub>х<sub>2</sub> =`х₁`х<sub>2</sub> Ú`х₁х₂ Ú`х₁ Ú х₁х₂ =

=`х<sub>1</sub>`х₂ Ú`х<sub>1</sub>х<sub>2</sub> Ú`х₁ Ú х₁х₂ Ú х₂ = `х₁ Ú х₂.

Теперь перейдем ко второму этапу получения минимальной ДНФ.

Пусть дана сокращённая ДНФ функции f(x₁,..., x_n):

N = U₁ Ú U₂ Ú … Ú U_k. Простой импликант называется ядерным (входящим в ядро функции f(x₁,..., x_n)), если

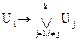≢ 1.

Эта запись означает, что простой импликант U_i является ядер­ным импликантом функции f(x₁,..., x_n), если существует набор a = (a₁,..., a_n), на котором импликант U_i обращается в 1, а все ос­тальные импликанты сокращённой ДНФ – в ноль.

Пример 2. Найти ядерные импликанты функции
f(x₁,..., x_n), заданной своей сокращённой ДНФ:

`х<sub>2</sub>`х₄ Ú х₁`х<sub>4</sub> Ú х<sub>1</sub> х<sub>2</sub> Ú х<sub>2</sub> х<sub>3</sub> х<sub>4</sub> Ú`х₁ х₃ х₄ Ú`х<sub>1</sub>`х₂ х₃.

Простой импликант х₂`х<sub>4</sub> является ядерным, так как на наборе (0,0,0,0) `х₂`х₄ = 1, а дизъюнкция оставшихся импликантов:

х₁`х<sub>4</sub> Ú х<sub>1</sub> х<sub>2</sub> Ú х<sub>2</sub> х<sub>3</sub> х<sub>4</sub> Ú`х₁ х₃ х₄ Ú`х<sub>1</sub>`х₂ х₃ = 0.

Простой импликант х₁`х₄ – неядерный, так как он равен еди­нице на наборах {1,0,0,0}, {1,0,1,0}, {1,1,0,0}, {1,1,1,0}, но на этих же наборах:

`х<sub>2</sub>`х₄ Ú х₁ х₂ Ú х₂ х₃ х₄ Ú`х<sub>1</sub> х<sub>3</sub> х<sub>4</sub> Ú`х₁`х₂ х₃ =1,

следовательно

х₁`х<sub>4</sub> ®`х₂`х<sub>4</sub> Ú х<sub>1</sub> х<sub>2</sub> Ú х<sub>2</sub> х<sub>3</sub> х<sub>4</sub> Ú`х₁ х₃ х₄ Ú`х<sub>1</sub>`х₂ х₃ º 1.

Простой импликант х₁ х₂ – ядерный, т.к. на {1,1,0,1}:
х₁ х₂ = 1, а`х<sub>2</sub>`х₄ Ú х₁`х<sub>4</sub> Ú х<sub>2</sub> х<sub>3</sub> х<sub>4</sub> Ú`х₁ х₃ х₄ Ú `х<sub>1</sub>`х₂ х₃ = 0.

Простой импликант х₂ х₃ х₄ – неядерный, так как на наборах {0,1,1,1}, {1,1,1,1}:

`х<sub>2</sub>`х₄ Ú х₁`х<sub>4</sub> Ú х<sub>1</sub> х<sub>2</sub> Ú`х₁ х₃ х₄ Ú`х<sub>1</sub>`х₂ х₃ = 1.

Простой импликант `х₁ х₃ х₄ – неядерный, так как на наборах {0,0,1,1}, {0,1,1,1}:

`х<sub>2</sub>`х₄ Ú х₁`х<sub>4</sub> Ú х<sub>1</sub> х<sub>2</sub> Ú х<sub>2</sub> х<sub>3</sub> х<sub>4</sub> Ú`х₁`х₂ х₃ = 1.

Простой импликант `х<sub>1</sub>`х₂ х₃ – неядерный, так как на наборах {0,0,1,0}, {0,0,1,1}:

`х<sub>2</sub>`х₄ Ú х₁`х<sub>4</sub> Ú х<sub>1</sub> х<sub>2</sub> Ú х<sub>2</sub> х<sub>3</sub> х<sub>4</sub> Ú `х₁ х₃ х₄ = 1.

Теорема 8 (без доказательства). Простой импликант U_i входит во все тупиковые ДНФ тогда и только тогда, когда U_i входит в ядро функции f(x₁,..., x_n), то есть тогда и только тогда, когда он явля­ется ядерным.

Следствие. Пусть ядро f(x₁,..., x_n) состоит из импли­кантов U_l1,...,U_lm тогда импликант U_l, для которого выпол­нено соотношение: 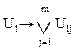º 1.

То есть, импликант U_l обращается в единицу на тех же набо­рах, что и дизъ­юнкция ядерных импликантов: не входит ни в одну из тупиковых ДНФ функции f(x₁,..., x_n).

Возвращаясь к примеру 2, отметим, что:

Импликант х₁`х₄ удов­летворяет следствию из теоремы 8:

х₁`х<sub>4</sub> ®`х₂`х₄ Ú х₁ х₂ º 1

и по­этому не входит ни в одну тупиковую форму.

Импликант х₂ х₃ х₄, для которого

х₂ х₃ х₄ ®`х<sub>2</sub>`х₄ Ú х₁ х₂ ≢ 1 не удовлетворяет следствию.

Импликант`х<sub>1</sub>х<sub>3</sub>х<sub>4</sub>, для которого`

`х<sub>1</sub> х<sub>3</sub> х<sub>4</sub>®`х₂`х₄ Ú х₁ х₂ ≢ 1, не удовлетворяет следствию.

Импликант`х<sub>1</sub>`х₂х₃, для которого

`х<sub>1</sub>`х₂ х₃®`х<sub>2</sub>`х₄ Ú х₁ х₂ ≢ 1, не удовлетворяет следствию.

Таким образом, последовательность действий при выполнении второго этапа состоит в следующем:

1) для каждого простого импликанта сокращённой ДНФ про­верить, входит он в ядро или нет. Отметить неядерные импликанты;

2) проверить для отмеченных импликантов выполне­ние следствия из теоремы 8. Простые импликанты, для которых выпол­нено следствие, удалить из сокращённой ДНФ;

3) проверить возможность удаления оставшихся отмечен­ных конъюнкций. Из полученных тупиковых ДНФ выбрать минималь­ную ДНФ.

Рассмотрим эту последовательность действий на примере 2.

1) нашли ядро функции f(х₁, х₂, х₃, х₄), состоящее из простых импликантов `х<sub>2</sub>`х₄ и х₁ х₂. Отметим курсивом в сокращённой ДНФ неядерные импликанты:

`х<sub>2</sub>`х₄ Ú х₁`х<sub>4</sub> Ú х<sub>1</sub> х<sub>2</sub> Ú х<sub>2</sub> х<sub>3</sub> х<sub>4</sub> Ú` х₁ х₃ х₄ Ú` х<sub>1</sub>`х₂ х₃;

2) среди помеченных импликантов нашли удовлет­воряющий следствию из теоремы 8. Это импликант х₁`х₄. Удалим его из со­кращённой ДНФ:

`х<sub>2</sub>`х₄ Ú х₁ х₂ Ú х₂ х₃ х₄ Ú` х<sub>1</sub> х<sub>3</sub> х<sub>4</sub> Ú` х₁`х₂ х₃;

3) для получения тупиковых ДНФ удаляем подмно­жества от­меченных импликантов. Можно удалить следующие подмножества:

{х₂ х₃ х₄,`х<sub>1</sub> х<sub>3</sub> х<sub>4</sub>,`х₁`х<sub>2</sub> х<sub>3</sub>}<sup>I</sup>, { х<sub>2</sub> х<sub>3</sub> х<sub>4</sub>,`х₁ х₃ х₄}^II, { х₂ х₃ х₄, `х<sub>1</sub>`х₂ х₃}^III, {`х<sub>1</sub> х<sub>3</sub> х<sub>4</sub>,`х₁`х<sub>2</sub> х<sub>3</sub>}<sup>IV</sup>, {x<sub>2</sub> x<sub>3</sub> x<sub>4</sub> }<sup>V</sup>, {`х₁ х₃ х₄}^VI, {`х<sub>1</sub>`х₂ х₃} ^VII.

При каждом удалении нужно проверять, представляет ли оставшаяся ДНФ функцию f(х₁, х₂, х₃, х₄).

Если удалить подмножество I, то получим ДНФ, не представ­ляющую функцию f(х₁, х₂, х₃, х₄), так как на наборе {0,1,1,1} функ­ция:

f (х₁, х₂, х₃, х₄) = 1, а `х<sub>2</sub>`х₄ Ú х₁х₂ = 0.

Если удалить подмножество II, то получим ДНФ, не представ­ляющую функцию f(х₁, х₂, х₃, х₄), так как на наборе {0,1,1,1} функ­ция

f(х₁, х₂, х₃, х₄) = 1, а `х<sub>2</sub>`х₄ Ú х₁ х₂ Ú `х<sub>1</sub>`х₂ х₃ = 0.

Если удалить подмножество III, получим минимальную ДНФ функции f(x₁, x₂, х₃, х₄):

`х<sub>2</sub>`х₄ Ú х₁ х₂ Ú`х₁ х₃ х₄ – минимальная ДНФ.