Рекуррентные соотношения

ЛЕКЦИЯ № 11

В комбинаторных задачах искомым решением часто является числовая последовательность u₁, u₂, …, u_n, … Например, если мы ищем число подмножеств m-элементного множества, то 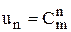. В данном разделе рассмотрим ситуацию, при которой свойства членов искомой последовательности определяются некоторым рекуррентным соотношением, которому удовлетворяют числа u_n:

u_{n + k} + b₁ u_{n + k – 1} + b₂ u_{n + k – 2} +…+ b_k u_n = 0, (3.6)

где b₁, b₂, …, b_k – некоторые коэффициенты. Выражение (3.6) называется еще разностным линейным уравнением k-го порядка с постоянными коэффициентами.

Одной из наиболее известных последовательностей, задаваемых линейным рекуррентным соотношением, является последовательность Фибоначчи {F_n}, определяемая следующими условиями: F₀ = 0; F₁ = 1; F_n+2 = F_n+1 + F_n. Отсюда получаем F₂ = 1; F₃ = 2; F₄ = 3; F₅ = 5; F₆ = 8 и т.д.

Воспользовавшись уравнением (2.8) всегда можно вычислить значения u_n для любых n, если знать первые k членов последовательности. Однако, часто необходимо знать явную формулу для вычисления u_n.

Теорема 3.4. Пусть l₁, l₂,…, l_s – корни соответствующих кратностей m₁, m₂,…, m_s характеристического уравнения для выражения (3.6):

l^k + b₁ l^k–1 + b₂ l^k–2 +…+ b_k = 0 (3.7)

Тогда общее решение уравнения (3.6) определяется по формуле:

u_n = (C₁₁ + C₁₂ ×n + C₁₃×n² + … + )+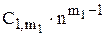

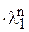(C₂₁ + C₂₂ ×n + C₂₃×n² + … + 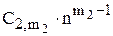)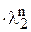+ … (3.8)

(C_s,1 + C_s,2 ×n + C_s,3×n² + … + ),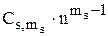

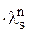где C₁₁,…, 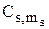– константы (их число равно k), определяемые начальными условиями.

Пример 3.3. Решим уравнение Фибоначчи F_n+2 – F_n+1 – F_n = 0. Его характеристическое уравнение имеет вид: l² – l – 1 = 0. Корни равны 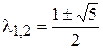– некратные. Обозначим Ф₁ = l₁ » 1.618; Ф₂ = l₂ » – 0.618. Общее решение равно:

.

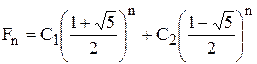Из начальных условий F₀ = 0; F₁ = 1 получаем систему уравнений для вычисления С₁ и С₂ = 1:

.

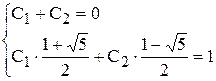Отсюда С₁ = – С₂ = .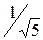

Использование рекуррентных соотношений дает эффективный метод решения многих комбинаторных задач.

Пример 3.4. Найти число бинарных n-последовательностей, в которых никакие две единицы не стоят рядом.

Решение. Обозначим:

z_n – число искомых последовательностей;

х_n – число последовательностей, заканчивающихся 0;

у_n – число последовательностей, заканчивающихся 1.

Назовем для краткости последовательность, заканчивающуюся 0 – х-последовательностью, а заканчивающихся 1 – у-последовательностью.

Очевидны следующие их свойства.

1) х-последовательность длиной n можно получить, приписав 0 в конец либо у-последовательности либо х-последовательности длиной n – 1.

2) у-последовательность длиной n можно получить, приписав 1 только в конец х-последовательности длиной n – 1.

Отсюда имеем следующую систему уравнений:

.

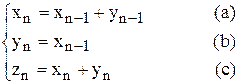Уравнение (a) отражает свойство 1), уравнение (b) – свойство 2), а уравнение (а) соответствует очевидному равенству.

Из уравнения (b) при замене n на n – 1 имеем: у_n–1 = х_n–2.

Подставим это равенство в (a), получим: х_n = х_n–1 + х_n–2, т.е. числа х_n образуют последовательность Фибоначчи. Вычтем (b) из (a), получим:

х_n – у_n = у_n–1 Þ х_n = у_n + у_n–1 Þ у_n+1 = у_n + у_n–1

– тоже последовательность Фибоначчи. В соответствие с формулой общего решения и уравнением (c) получим:

.

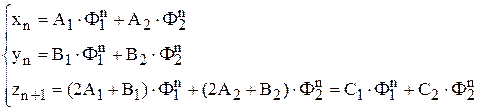Для нахождения констант запишем начальные условия. z₁ = 2, т.к. существует 2 последовательности длиной 1: 0 и 1. z₂ = 3, т.к. существует 3 последовательности длиной 2: (0 0), (0 1), (1 0). Отсюда 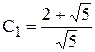; 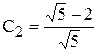. Следовательно

_.

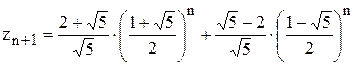Например, z₉ = 89, z₁₉ = 10946.