Связь производящих функций с линейными рекуррентными
Пусть имеем дробно-рациональную функцию
f(x) = 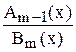 =
= 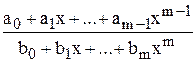 ,
,
которая разлагается в ряд f0 + f1x + f2 x + …. Отсюда A(x) = B(x)×f(x). Подставим вместо f(х) ее ряд – получим систему уравнений:
b0 f0 = a0;
b0 f1 + b1 f0 = a1;
b0 f2 + b1 f1 + b2 f0 = a2;
………………………..
b0 fm –1 + b1 fm –2 +… + bm –1 f0 = am – 1;
b0 fm + b1 fm –1 +… + bm f0 = 0;
………………………………..
b0 fm + n + b1 fm –1 + n +… + bm fn = 0;
……………………………
Во всех уравнениях, начиная с m+1-го, правая часть равна 0, т.к. am + 1 = … = am + n =…= 0. Следовательно, имеем линейное рекуррентное соотношение
b0 fm + n + b1 fm –1 + n +… + bm fn = 0, (3.13)
которому удовлетворяют члены ряда для функции f(x). Таким образом, мы получили теорему о связи производящих функций с линейными рекуррентными соотношениями:
Теорема 3.5. Для того, чтобы производящая функция числовой последовательности была правильной рациональной дробью необходимо и достаточно, чтобы члены этой последовательности удовлетворяли линейному рекуррентному соотношению, характеристическое уравнение которого совпадает со знаменателем этой дроби, записанным в обратном порядке.
Пример 3.10. Найдем производящую функцию для чисел Фибоначчи.
Решение. Имеем рекуррентное соотношение: Fn+2 – F n+1– Fn = 0. Следовательно, f(x) = 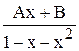 . A и В легко найти с помощью деления многочленов:
. A и В легко найти с помощью деления многочленов:
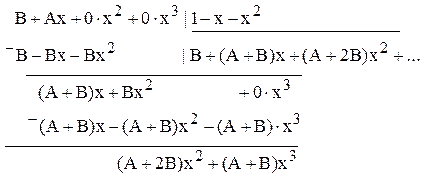
Следовательно, 0 = F0 = B; 1 = F1 = A + B, т.е. В = 0; А = 1 или 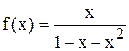 .
.
 2014-02-18
2014-02-18 750
750








