Ускорение точки при естественном способе

задания движения

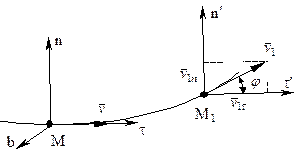Пусть точка движется по криволинейной траектории. Рассмотрим два ее положения в моменты времени t (s, M, v) и t ₁ (s ₁, M₁, v ₁).

Ускорение при этом определяется через его проекции на оси естественной системы координат, движущейся вместе с точкой M. Оси при этом направлены следующим образом:

M t - касательная, направлена вдоль касательной к траектории, в сторону положительного отсчета расстояния,

M n – главная нормаль, направлена по нормали, лежащей в соприкасающейся плоскости, и направлена в сторону вогнутости траектории,

M b – бинормаль, перпендикулярна плоскости M tn и образует с первыми осями правую тройку.

Так как вектор ускорения лежит в соприкасающейся плоскости, то a_b= 0. Найдем проекции ускорения на другие оси.

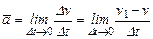. (19)

Спроектируем (19) на координатные оси

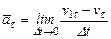, (20)

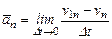. (21)

Проведем через точку M₁ оси параллельные осям в точке M и найдем проекции скорости:

Mt: ,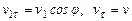

Mn: 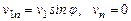, (22)

где j - так называемый угол смежности.

Подставляем (22) в (20)

.

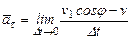При Dt® 0 j® 0, cosj® 1, тогда

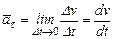
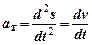. (23)

Касательное ускорение точки определяется первой производной по времени от скорости или второй производной по времени от криволинейной координаты.

Касательное ускорение характеризует изменение вектора скорости по величине.

Подставим (22) в (21)

.

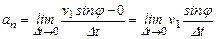Умножим числитель и знаменатель на DsDj чтобы получить известные пределы

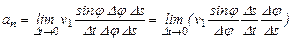, (24)

где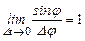(первый замечательный предел),

,,

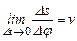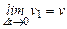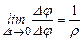, где r - радиус кривизны траектории.

Подставляя вычисленные пределы в (24), получим

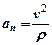. (25)

Нормальное ускорение точки определяется отношением квадрата скорости к радиусу кривизны траектории в данной точке.

Нормальное ускорение характеризует изменение вектора скорости по направлению и всегда направлено в сторону вогнутости траектории.

Окончательно получим проекции ускорения материальной точки на оси естественной системы координат и модуль вектора

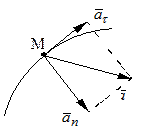
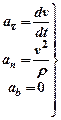, (26)

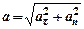. (27)