Метод наименьших квадратов. Теорема Гаусса-Маркова

Как и в случае регрессионного уравнения с одной переменной, целью метода является выбор вектора оценок b, минимизирующего сумму квадратов остатков e_t (квадрат длины вектора остатков e):

.

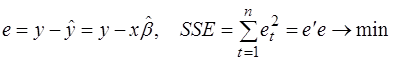Выразим e`e через x и b:

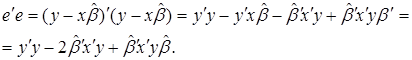
(44)

Необходимые условия минимума SSE получаются дифференцированием уравнения (44) по вектору b:

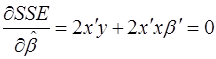, (45)

откуда, учитывая обратимость матрицы X`X, находим оценку метода наименьших квадратов:

b_OLS = (x`x)<sup>-1</sup> x`y. (46)

Покажем, что, как и в случае одного регрессора, формула (45) означает, что вектор остатков e ортогонален всем независимым переменным x₁,…,x_k (столбцам матрицы X). Условие x₁e =…= x`<sub>k</sub>e = 0 эквивалентно равенству x`e = 0.

Действительно,

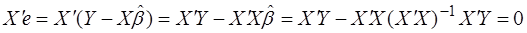. (47)

Получим полезную в дальнейшем формулу для суммы квадратов остатков:

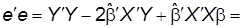
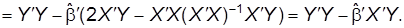(48)

Геометрическая интерпретация в основном совпадает с геометрической интерпретацией регрессионного уравнения с одной независимой переменной.

Представим Y, x₁, …, x_k как векторы в n-мерном евклидовом пространстве Rⁿ. Векторы x₁, …,_.x_k образуют k-мерное подпространство p.

Вектор 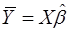есть ортогональная проекция вектора Y на гиперплоскость p.

Вектор остатков e = y - y ортогонален подпространству p.

Как и в случае регрессионного уравнения с одной независимой переменной, можно показать, что оценка метода наименьших квадратов является оптимальной.