2014-02-24
5031. Оператор замыкания.
Def. Множество Т снабжённое оператором замыкания Cl (abbreviation of Closure), определённом на множестве всех подмножеств множества Т называется топологическим пространством, если этот оператор удовлетворяет следующим условиям:
1. Cl(XÈY}= Cl(X)ÈCl(Y) "X,YÎT (аддитивность)
2. Cl(X)ÊX "XÎT (монотонность)
3. Cl(Cl(X))=Cl(X) («проективность»)
4. Cl(Æ)=Æ.
5. Cl({а})={а} для любого одноэлементного (точечного) множества {а}.
Замечания.
На самом деле, только первые четыре свойства этого оператора являются обязательными для самого общего определения топологического пространства. Добавление пятого свойства выделяет более узкий класс топологических пространств – так называемых Т1- пространств. Для наших с вами целей, разумеется, и этот класс является ещё слишком широким.
С другой стороны эти пять условий не являются независимыми.
Например, условие 2 следует из условий 1 и 5, а условие 4 также следует из них, если только исходное Т1-пространство содержит хотя бы две точки.
Упражнение 1. Докажите оба эти утверждения.
Далее, нам постоянно придётся одновременно с оператором замыкания иметь дело и с оператором взятия теоретико-множественного дополнения, которое мы ранее обозначали чертой сверху над множеством. Проблема в том, что в английском языке «дополняющий» тоже начинается с буквы «с» - complementary. Поэтому общепринято также для оператора замыкания, помимо обозначения Cl использовать то, что мы ранее использовали для обозначения дополнения, а именно, черту сверху, а для дополнения будем теперь использовать символ с. В тех случаях, когда мы используем композиции из этих операций, мы записываем их сверху и справа от множества последовательно. Например, Хс-с означает, что мы замыкаем дополнение к Х, а затем переходим к дополнению того, что получили;
Х-с- говорит о том, что мы имеем дело с замыканием дополнения к замыканию Х.
В обозначениях с чертой вышеперечисленные пять условий выглядят так:
|
|
|
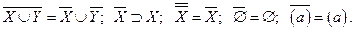
Упражнение 2.
Выведите из одного только первого свойства следующие утверждения:
2.1.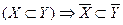 
2.2.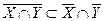 
(hint: take advantage of the formula (XÌY)Û(Y=XÈY)); rely on 2.1 dealing with 2.2)
Упражнение 3.
Для любого множества М индексов t (счётного или несчётного) докажите формулы:
; 
.
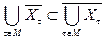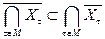Упражнение 4.
Докажите следующие утверждения: Cl(T)=T; (X – конечное множество)ÞCl(X)=X.
Упражнение 5.
Докажите, что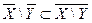 
. (hint: start with identity XÈY=(X\Y)ÈY; intersect then both sides of equation with Y-c)
Def. Неподвижные точки (подмножества топологического пространства Т) оператора замыкания называются замкнутыми подмножествами.
Иными словами, подмножество Х замкнуто Û Cl(X)=X.
Множество ХÌТ называется открытым, если его дополнение замкнуто.
|
|
|
Упражнение 6.
а) Объединение конечного числа замкнутых множеств замкнуто;
б) Пересечение любого семейства замкнутых множеств замкнуто;
в) Объединение любого семейства открытых множеств открыто;
г) Пересечение конечного числа открытых множеств открыто.
Замечание.
Чаще в литературе именно понятие открытого множества используется как первоначальное при определении топологических пространств. Точнее, топологическим пространством называется множество вместе с выделенной в нём системой подмножеств (называемых открытыми), обладающей тем свойством, что пересечение любого конечного числа таких множеств, а также и объединение любого семейства этих множеств снова принадлежат этой системе (т.е., являются открытыми). То есть, доказанные вами последние два свойства кладутся в основу определения топологического пространства. Поскольку допускаются и пустые семейства подмножеств, то пустое множество и само пространство Т являются открытыми. А замкнутыми, по определению, называются множества, дополнительные к открытым. Определение топологических пространств с помощью оператора замыкания принадлежит польскому топологу Казимиру Куратовскому.
Упражнение 7.
G открыто Þ "Х GÇCl(X)ÌCl(GÇX) и, соответственно, Cl(GÇCl(X))=CL(GÇX).
Выражение (Т,Е) образуют топологическую пару, означает, что Е просто является подмножеством топологического пространства (ТП) Т. Говорят, что (Т,Е,Х) образуют топологическую тройку, если ТÉЕÉХ. И так далее – множества образуют этакую «матрёшку». Рассмотрим такую тройку, в которой Т и Е фиксированы, а Х – переменная величина. Естественно назвать замыканием Х в Е (относительным замыканием) пересечение замыкания Х в Т с Е: ClEX=CL(X)ÇE.
Если полученный оператор ClE окажется оператором замыкания в Е, то Е, тем самым, превратится в топологическое подпространство пространства Т.
Упражнение 8. Проверьте, что это, действительно, именно так.
Упражнение 9. Пусть (Т, Е, G, X) – топологическая четвёрка.
Совпадают ли топология, наследуемая G из Е (как подмножества ТП Е) с топологией, наследуемой прямо из Т (как подмножества Т)? Иными словами, является ли подпространство топологического подпространства Т само топологическим подпространством (ТПП) Т?
По-другому это же можно сформулировать ещё и так:
обладает ли свойство «быть подпространством» транзитивностью, подобно тому как этим обладает свойство «быть подмножеством», например.
Следующее упражнение без ущерба для понимания дальнейшего материала может быть пропущено. Упражнение 10*. (Задача Куратовского)
Пусть(Т,Е) образуют топологическую пару.
Сколько (самое большее) различных множеств можно получить, (считая Т и Е) применяя попеременно операторы замыкания и дополнения?
Def. Границей множества Х называется множество Fr(X)=Cl(X)ÇCL(Xc). Внутренностью множества Х называется множество Int(X)=Xc-c.
Упражнение 11. Докажите следующие формулы:
11.1. Int(XÇY)=Int(X)ÇInt(Y); 11.6. Fr(X)=(XÇXc-)È(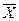
\X);
11.2. (XÌY)ÞInt(X)ÌInt(Y); 11.7. 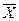=XÈFr(X);
11.3. Fr(Xc)=Fr(X); 11.8. Int(Int(X))=Int(X);
11.4. Int(X)=X\Xc-=X\Fr(X); 11.9. Int(X)ÇFr(X)=Æ;
11.5. Fr (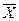)ÌFr(X); 11.10. Fr(Int(X))ÌFr(X).
Def. Базой ТП Т называется такое семейство открытых множеств Г, что всякое открытое множество в Т представимо в виде объединения множеств из Г.
Семейство открытых множеств S называется подбазой или предбазой ТП Т, если пересечения всевозможных конечных наборов множеств из S составляет базу ТП Т.
Если в ТП Т существует база, состоящая из счётного числа множеств, то тогда оно называется пространством сосчётной базой.
