Неравенство Коши - Буняковского

Теорема. Для любых векторов и справедливо неравенство

.

Доказательство. Так как скалярное произведение является положительно определенной формой, то

.

При фиксированных векторах и мы имеем квадратный трехчлен от , дискриминант которого отрицательный или равен нулю:

.

Отсюда или . Теорема доказана.

Следствие (неравенство треугольника). Для любых векторов и справедливо неравенство

.

Доказательство.

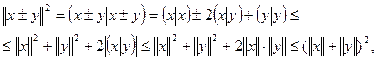
следовательно, .

16.4. Угол между векторами. Заметим, что из неравенства Коши - Буняковского следует, что

.

Это значит, что отношение является косинусом вполне определенного угла :

.

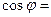
Этот угол принято считать углом между векторами.

Определение. Векторы и называются ортогональными, если угол между ними равен , т.е. .

Нулевой вектор ортогонален любому вектору.

Заметим, что из ортогональности векторов и следует теорема Пифагора:

.

Эту теорему можно обобщить на любое число попарно ортогональных векторов:

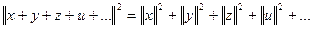
Задача. Докажите, что если , то векторы и ортогональны (диагонали ромба пересекаются под прямым углом).