Понятие квадратичной формы

II. Квадратичные формы и квадрики

Определение 1: формой или однородным многочленом от нескольких переменных называется многочлен, степени всех одночленов которого одинаковы. Если эта степень первая, то форма называется линейной, если вторая, то форма называется квадратичной: 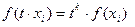- однородная функция степени .

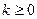Линейная форма от 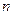переменных 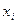имеет вид:

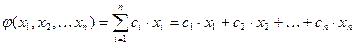
Квадратичная форма от этих же переменных имеет вид:

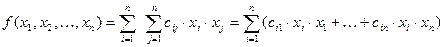(1)

причём полагают .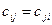

Пример: n = 2

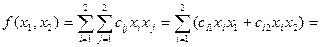
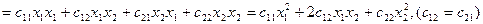
Определение 2: квадратная матрица из коэффициентов 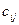квадратичной формы от 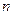переменных вида 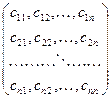называется матрицей квадратичной формы (1).

Так как 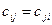, то эта матрица симметрическая: её элементы, симметричные относительно главной диагонали, равны между собой.

Определение 3: линейным преобразованием переменных называется переход от системы 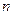переменных 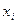к системе 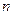переменных 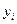по формулам:

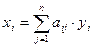(2)

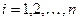где и 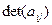≠0, (3)

то есть матрица из коэффициентов 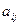является невырожденной.

Замечания: 1) легко видеть, что множество всех указанных линейных преобразований является группой относительно их последовательного выполнения, то есть относительно композиции;

2) переменные 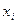можно рассматривать как координаты некоторого вектора 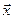векторного пространства 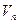, либо как координаты некоторой точки Х связанного с ним аффинного пространства 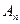. Тогда в первом случае формула (2) при условии (3) есть формула перехода к новому базису пространства 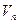, а во втором случае – формулы перехода к новой аффинной системе координат с прежним началом (отсутствуют свободные члены);

3) мы ограничимся рассмотрением квадратичных форм и линейных преобразований лишь с действительными коэффициентами и переменными: ;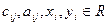

4) подвергнув переменные 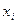в квадратичной форме (1) линейному преобразованию (2) при условии (3), получим также квадратичную от переменных 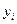с новыми коэффициентами. Оказывается, что преобразование (2) всегда можно выбрать так, что новая квадратичная форма будет содержать только квадраты новых переменных:

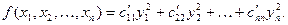(4)

(некоторые коэффициенты 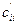могут оказываться нулевыми).

Определение 4: вид (4) квадратичной формы (1) называется её каноническим (простейшим) видом.

Очевидно, матрицы 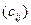квадратичной формы канонического вида является диагональной: .

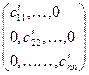Если при этом коэффициенты 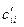равны 0 или ±1, то говорят, что квадратичная форма имеет нормальный вид.