Для реализации окон в среде MATLAB используется множество встроенных функций.
1. Прямоугольное окно.
Функция 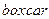 , реализующая «прямоугольное окно», введена в
, реализующая «прямоугольное окно», введена в 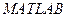 лишь для полноты набора весовых функций, поскольку она соответствует отсутствию взвешивания:
лишь для полноты набора весовых функций, поскольку она соответствует отсутствию взвешивания:
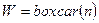
Возвращаемый вектор заполнен единицами: 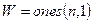 ,
, 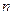 – его длина.
– его длина.
2. Треугольное окно.
Функция 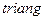 реализует треугольное окно:
реализует треугольное окно:
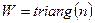
Отсчеты треугольного окна рассчитываются по формулам:
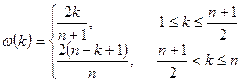 – для нечетных
– для нечетных 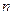
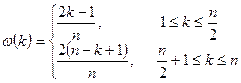 – для четных
– для четных 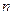
При нечетном 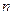 треугольное окно является симметричным, его крайние значения (при
треугольное окно является симметричным, его крайние значения (при 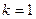 и
и 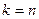 ) равны
) равны 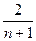 , а в середине окна (при
, а в середине окна (при 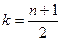 ) достигается единичное значение.
) достигается единичное значение.
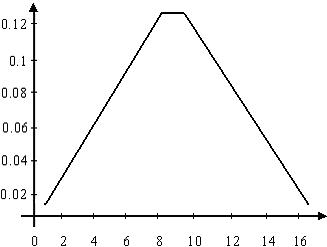
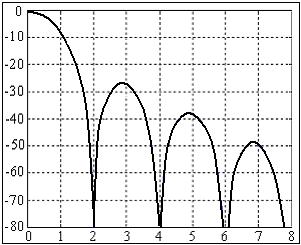
а) треугольное окно б) амплитудный спектр треугольного окна
Рис 2. Треугольное окно и его амплитудный спектр.
3. Окно Бартлетта.
Функция 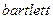 реализует окно Бартлетта:
реализует окно Бартлетта:
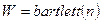 .
.
Окно Бартлетта, по сути, является треугольным, но рассчитывается несколько иначе:
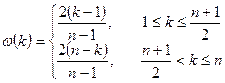 – для нечетных
– для нечетных 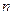
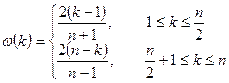 – для четных
– для четных
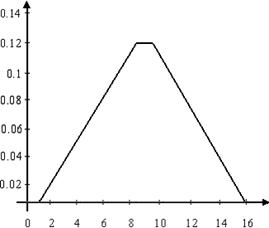
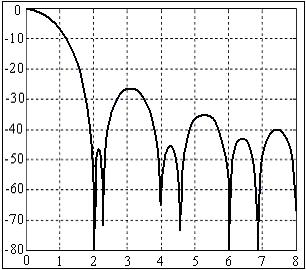
а) окно Бартлетта б) амплитудный спектр окна Бартлетта.
Рис 3. Окно Бартлетта и его амплитудный спектр.
В отличие от треугольного окна, значения окна Бартлетта по краям (при 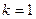 и
и 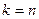 ) равны нулю. Кроме того, независимо от четности
) равны нулю. Кроме того, независимо от четности 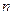 оно является симметричным. Окно Бартлетта представляет собой отсчеты симметричного треугольного импульса, который начинается при
оно является симметричным. Окно Бартлетта представляет собой отсчеты симметричного треугольного импульса, который начинается при 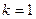 , заканчивается при
, заканчивается при 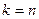 и имеет единичную амплитуду. Максимум значения достигается при
и имеет единичную амплитуду. Максимум значения достигается при 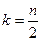 , поэтому при нечетном
, поэтому при нечетном 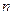 окно Бартлетта не достигает единичного значения в середине. При нечетном
окно Бартлетта не достигает единичного значения в середине. При нечетном 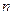 ненулевые отсчеты окна Бартлетта совпадают с отчетами треугольного окна длины
ненулевые отсчеты окна Бартлетта совпадают с отчетами треугольного окна длины 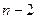 .
.
4. Окно Хана.
Функция 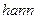 реализует окно Хана:
реализует окно Хана:
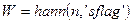 .
.
Строковый параметр 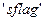 позволяет выбрать режим расчета окна.
позволяет выбрать режим расчета окна.
В симметричном случае, принятом по умолчанию, отсчеты окна Хана рассчитываются по формуле:
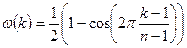 .
.
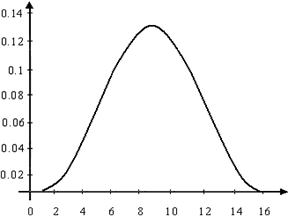
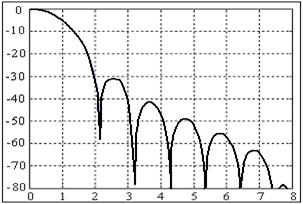
а) окно Хана б) амплитудный спектр окна Хана
Рис 4. Окно Хана и его амплитудный спектр.
5. Окно Хэмминга.
Функция 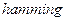 реализует окно Хемминга:
реализует окно Хемминга:
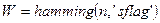 .
.
В симметричном случае отсчеты окна Хемминга рассчитываются по формуле:
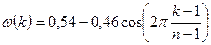 .
.
Для периодического варианта 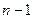 в знаменателе формулы заменяется на
в знаменателе формулы заменяется на 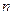 (возможна и другая трактовка: выполняется расчет по приведенной формуле для окна длиной
(возможна и другая трактовка: выполняется расчет по приведенной формуле для окна длиной 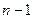 , а затем последний элемент отбрасывается).
, а затем последний элемент отбрасывается).
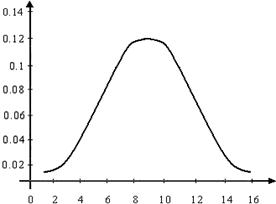
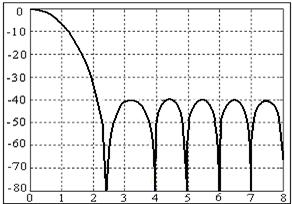
а) Окно Хэмминга б) амплитудный спектр окна Хэмминга
Рис 5. Окно Хэмминга и его амплитудный спектр.
6. Окно Блекмана.
Функция 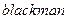 реализует окно Блекмана:
реализует окно Блекмана:
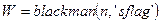 .
.
В симметричном случае отсчеты окна Блекмана рассчитываются по формуле:
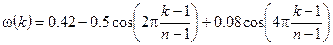 .
.
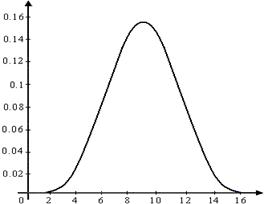
а) окно Блекмана б) амплитудный спектр окна Блекмана
Рис 6. Окно Блекмана и его амплитудный спектр.
7. Окно Чебышева.
Функция 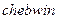 реализует окно Чебышева:
реализует окно Чебышева:
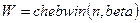 .
.
Здесь 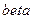 – степень подавления боковых лепестков в децибелах. Для окна Чебышева все боковые лепестки имеют одинаковый, заданный при расчете окна уровень. Отсчеты окна Чебышева рассчитываются путем вычисления обратного преобразования Фурье от его частотной характеристики:
– степень подавления боковых лепестков в децибелах. Для окна Чебышева все боковые лепестки имеют одинаковый, заданный при расчете окна уровень. Отсчеты окна Чебышева рассчитываются путем вычисления обратного преобразования Фурье от его частотной характеристики:
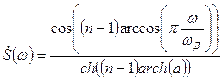 , где
, где 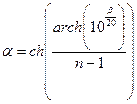 .
.
Здесь 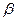 – степень подавления боковых лепестков в децибелах,
– степень подавления боковых лепестков в децибелах, 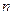 – требуемое количество отсчетов окна.
– требуемое количество отсчетов окна.
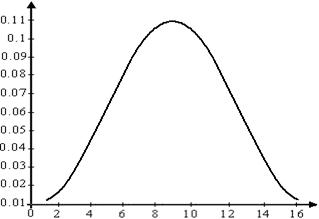
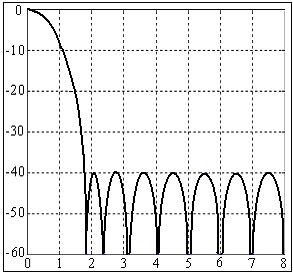
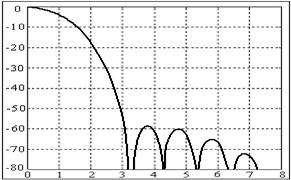
а) окно Чебышева б) амплитудный спектр окна Чебышева
Рис 7. Окно Чебышева и его амплитудный спектр.
Из графиков видно, что при 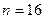 уровень боковых лепестков
уровень боковых лепестков 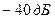 . Как обычно, с уменьшением уровня боковых лепестков главный лепесток расширяется.
. Как обычно, с уменьшением уровня боковых лепестков главный лепесток расширяется.
 2014-02-24
2014-02-24 6352
6352








