Неравенство Маркова (лемма Чебышева)
Тема 7. Закон больших чисел
Известно, что нельзя заранее уверенно предвидеть, какое из возможных значений примет случайная величина в итоге испытания, - это зависит от многих причин, учесть которые невозможно. Однако оказывается, что при некоторых условиях суммарное поведение достаточно большого числа случайных величин утрачивает случайный характер и становится закономерным. Эти условия и составляют содержание закона больших чисел.
Рассмотрим неравенства Маркова и Чебышева.
Теорема. Если случайная величина  принимает только неотрицательные значения и имеет математическое ожидание
принимает только неотрицательные значения и имеет математическое ожидание 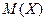 , то для любого положительного числа
, то для любого положительного числа  верно неравенство
верно неравенство
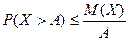 - неравенство Маркова.
- неравенство Маркова.
Доказательство. Рассмотрим дискретную случайную величину  . Расположим её значения в порядке возрастания. По отношению к числу
. Расположим её значения в порядке возрастания. По отношению к числу  значения случайной величины разбиваются на две группы: одни не больше числа
значения случайной величины разбиваются на две группы: одни не больше числа  , а другие больше
, а другие больше  .
.
I – группа II - группа
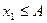
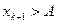
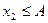
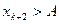
… …
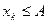
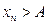
Найдём математическое ожидание:
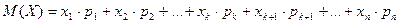 .
.
Так как все 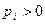 и по условию
и по условию 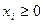 , то все члены правой части неотрицательны. Поэтому, если мы отбросим первые
, то все члены правой части неотрицательны. Поэтому, если мы отбросим первые 
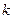 слагаемые в выражении
слагаемые в выражении 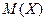 , получим неравенство:
, получим неравенство:
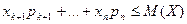 .
.
Заменив все оставшиеся значения случайной величины меньшей величиной  , получим более сильное неравенство:
, получим более сильное неравенство:
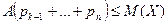 или
или 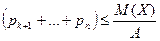 .
.
Сумма вероятностей 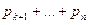 – это сумма вероятностей события
– это сумма вероятностей события 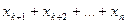 , то есть вероятность события
, то есть вероятность события 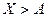 .
.
Следовательно, 
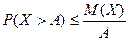 .
.
Так как события 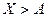 и
и 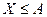 - противоположные, то
- противоположные, то
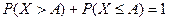 .
.
Подставляя в неравенство Маркова 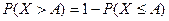 , получим другую форму неравенства Маркова:
, получим другую форму неравенства Маркова:
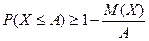 .
.
Теорема. Для любой случайной величины вероятность того, что отклонение случайной величины от её математического ожидания превзойдёт по абсолютной величине положительное число 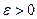 не больше дроби
не больше дроби
где 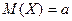 .
.
Доказательство. Пусть - случайная величина,
- случайная величина, 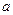 - её математическое ожидание. Тогда
- её математическое ожидание. Тогда  - случайная величина, которая не имеет отрицательных значений. Применим к ней неравенство Маркова, взяв за
- случайная величина, которая не имеет отрицательных значений. Применим к ней неравенство Маркова, взяв за 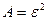 ,
,
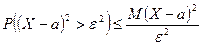 .
.
Так как неравенства 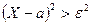 и
и 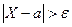 равносильны, а
равносильны, а 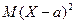 есть дисперсия случайной величины
есть дисперсия случайной величины  (по определению), то из последнего неравенства получим доказываемое неравенство:
(по определению), то из последнего неравенства получим доказываемое неравенство:
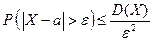 .
.
Так как события 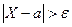 и
и 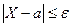 - противоположные, то
- противоположные, то
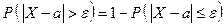 .
.
Подставив в неравенство Чебышева, получим другую форму неравенства Чебышева:
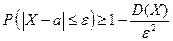 .
.
Пример 7.1. Вероятность производства нестандартной детали равна 0,1. Оценить с помощью неравенства Чебышева вероятность того, что из 10000 деталей число нестандартных окажется заключенным в границах от 950 до 1050.
Решение. Число нестандартных деталей – случайная величина  , распределенная
, распределенная
по биноминальному закону: n = 10000, p = 0,1, q = 0,9.
Математическое ожидание и дисперсия равны:
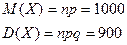 .
.
Неравенство 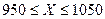 эквивалентно неравенству
эквивалентно неравенству 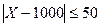 . Применим неравенство Чебышева при
. Применим неравенство Чебышева при 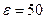 и
и 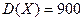
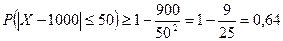 .
.
Т.е. вероятность того, что из 10000 деталей нестандартными окажется от 950 до 1050 не меньше 0,64.
Запишем неравенство Чебышева, используя вторую форму, для некоторых случайных величин.
1) Случайная величина распределена по биноминальному закону:
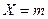 - число появления события в
- число появления события в  испытаниях,
испытаниях, 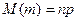 ,
, 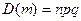 .
.
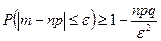 .
.
2) Производится n испытаний, в каждом из которых событие может произойти с одной и той же вероятностью р.
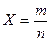 - частота появления события в
- частота появления события в  испытаниях,
испытаниях, 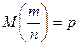 ,
, 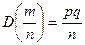 .
.
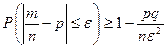 .
.
 2014-02-09
2014-02-09 1337
1337








