Сопряженные операторы в гильбертовом пространстве

Лекция 9 Сопряженные операторы в гильбертовом пространстве. Спектральное разложение самосопряженного компактного оператора

9.1. Сопряженные операторы в гильбертовом пространстве

9.2. Спектральное разложение самосопряженного компактного
оператора

Согласно теореме Рисса (теорема 4.1), каждый ограниченный линейный функционал f на гильбертовом пространстве H задается в виде скалярного произведения f (x) = (x, u), т. е. существует изометричное отображение между H и H', что позволяет реализовать сопряженный оператор как оператор в том же пространстве H. В случае комплексного пространства H соответствие f ® u между H и H' антилинейно. Поэтому свойства сопряженного оператора, полученного при такой реализации, несколько отличаются от свойств обычного сопряженного оператора A'. Вследствие этого, как правило, сопряженный оператор в гильбертовом пространстве определяют независимо.

Определение 9.1. Сопряженным оператором к оператору A : H ₁ ® H ₂, где H ₁ и H ₂ – гильбертовы пространства, называется оператор A^*: H ₂ ® H ₁ такой, что для любых x Î H ₁, y Î H ₂ выполняется равенство

.

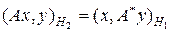Иногда, чтобы отличить его от сопряженного оператора A', оператор A^* называют эрмитово сопряженным.

Для эрмитово сопряженного оператора A^* справедливы все теоремы, доказанные для оператора A' (см. раздел 6.1). Отличие заметно только в свойстве операции сопряжения 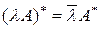(сравните с (l A) ' = (l A').

В случае гильбертовых пространств всегда A^** = A.

Определение 9.2. Линейный ограниченный оператор A : H ® H называется самосопряженным, если A = A^*, т. е. справедливо тождество (A x, y) =
= (x, A y). Линейный ограниченный оператор A называется унитарным, если A^* = A ^{– 1}. Линейный ограниченный оператор A называется нормальным, если A A^* = A^*A.

Эти определения имеют смысл только в гильбертовом пространстве, так как для банаховых пространств A и A' действуют в разных пространствах.

Пример 9.1. В пространстве C ⁿ со скалярным произведением 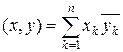рассмотрим оператор A : C ⁿ ® C ⁿ. Пусть оператор A задан матрицей (a_{i j}). Построим к нему сопряженный оператор A^*. Имеем

.

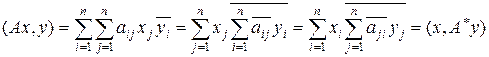Таким образом, оператору A^* соответствует матрица 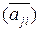– эрмитово сопряженная к матрице (a_{i j}). Оператор A самосопряжен, если 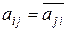, т. е. матрица (a_{i j}) эрмитово симметричная.

Пример 9.2. В пространстве L ₂ (T, m) со скалярным произведением

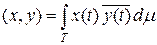
рассмотрим интегральный оператор 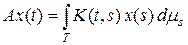, где K (t, s) Î
Î L ₂ (T ´ T). Тогда

.

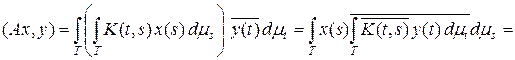
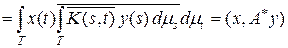Получаем, что сопряженный оператор

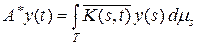
есть интегральный оператор с ядром 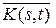. Интегральный оператор является самосопряженным, если .

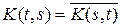Пример 9.3. В пространстве L ₂ [0, 1] рассмотрим оператор умножения на функцию a (t), т. е. Ax (t) = a (t) x (t). Тогда

.

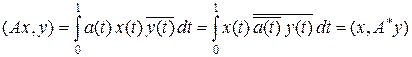Значит, 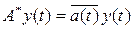. Если a (t) – вещественнозначная функция, то 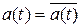и оператор A самосопряжен. Если | a (t) | = 1 почти всюду, то 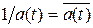и оператор A унитарный. Так как 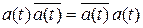, то оператор умножения на функцию нормальный.

Как известно из курса алгебры, эрмитово симметричная матрица (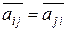) может быть ортогональным преобразованием приведена к диагональному виду. Наша цель – получить аналогичное утверждение для случая бесконечномерного пространства.

Приведем такую формулировку указанного свойства, которая имеет смысл в бесконечномерном пространстве: если A – самосопряженный оператор, то в пространстве H = C ⁿ существует ортогональный базис, состоящий из собственных векторов оператора A.

Понятие базиса, т. е. полной ортонормированной системы, имеется для гильбертовых пространств, и поэтому возникает вопрос, верно ли аналогичное утверждение для операторов в бесконечномерном гильбертовом пространстве.

Отметим прежде всего, что для произвольных операторов даже в конечномерном пространстве теорема не верна. Например, оператор, заданный матрицей 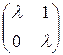в пространстве C², имеет только собственные векторы вида (0, x ₂), из которых нельзя построить базис в C². Покажем на примере, что в бесконечномерном случае аналогичная теорема не верна даже для самосопряженных операторов. В пространстве L ₂ [0, 1] рассмотрим оператор умножения на независимую переменную: Ax (t) = t x (t), A – самосопряженный оператор. Уравнение для нахождения собственных векторов имеет вид t x (t) = l x (t), откуда (t – l) x (t) = 0 и x (t) = 0. Значит, оператор A не имеет ни одного собственного вектора и тем более не существует базиса из собственных векторов.

Имеется два варианта обобщения этой теоремы на случай бесконечномерного пространства.

1. Выделение более узкого класса операторов, для которых теорема справедлива в приведенной формулировке.

2. Изменение формулировки (с ослаблением утверждения) так, чтобы теорема была верна для произвольного самосопряженного оператора.

В дальнейшем будет показано, что у любого компактного самосопряженного оператора в гильбертовом пространстве существует базис из собственных векторов, т. е. будет рассмотрен первый вариант обобщения.

Задача приведения эрмитово симметричной матрицы (a_{i j}) к диагональному виду в случае пространства C ⁿ эквивалентна приведению квадратичной формы 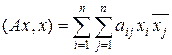к сумме квадратов.

По аналогии квадратичной формой оператора A будем называть числовую функцию j (x) = (Ax, x) на пространстве H. С оператором A можно связать также функцию двух переменных (Ax, y) – билинейную форму оператора A. Эта функция линейна по переменной x и, если A – самосопряженный оператор, антисимметрична:

,

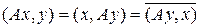т. е. обладает некоторыми свойствами скалярного произведения. Поэтому для нее выполнены некоторые тождества, которые аналогичны тождествам из утверждения 17.2 курса «Функциональный анализ. Часть 1»:

(A (x + y), x + y) + (A (x – y), x – y) = 2 (Ax, x) + 2 (Ay, y), (1)

(A (x + y), x + y) – (A (x – y), x – y) = 4 Re (Ax, y). (2)

Теорема 9.1. Пусть A – самосопряженный оператор в гильбертовом пространстве H. Тогда

1) квадратичная форма (Ax, x) принимает только вещественные значения, собственные значения оператора A вещественны;

2) собственные векторы оператора A, соответствующие различным собственным значениям, ортогональны;

3) для любого подпространства L Ì H, инвариантного относительно A, его ортогональное дополнение L ^{^} инвариантно относительно A.

Доказательство. 1. Первое утверждение вытекает из равенства 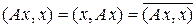. Пусть A x = l x, || x || = 1, тогда l = (A x, x) – вещественное число.

2. Если A x = l x и A y = m y, то (x, A y) = m (x, y), (A x, y) = l (x, y), откуда после вычитания получаем (l – m) (x, y) = 0. Если l ¹ m, то (x, y) = 0.

3. Пусть y Î L ^{^}. Тогда для любого x Î L имеем (x, A y) = (A x, y) = 0, что и означает A y Î L ^{^}, т. е. подпространство L ^{^} инвариантно относительно оператора A. Теорема доказана.

Теорема 9.2. Пусть A – самосопряженный оператор в гильбертовом пространства H. Тогда

1) ;

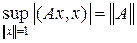2) существует спектральное значение l оператора A такое, что | l | = || A ||.

Доказательство. 1. Обозначим 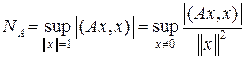, тогда

| (A x, x) | = N_A || x ||². (3)

Из неравенства | (A x, x) | £ || A x || || x || £ || A || || x ||² следует, что N_A £ || A || для любого ограниченного оператора. Используя тождество (2), неравенство (3), а затем тождество параллелограмма, получаем

Re (Ax, y) = (1/4) [ (A (x + y), x + y) – (A (x – y), x – y) ] £ (1/4) N_A ( || x + y ||² + || x – y ||² ) =
= (1/2) N_A (|| x ||² + || y ||²).

Положив y = ( || x || / || A x || ) A x, будем иметь || x || || A x || £ (1/2) N_A (|| x ||² + || x ||²), или || A x || £ N_A || x ||, откуда || A || £ N_A.

2. По доказанной части теоремы существует последовательность x_n Î H такая, что || x_n || = 1 и (A x_n, x_n) ® l, где l = || A || или l = – || A ||. Тогда

|| (A – l I) x_n ||² = (A x_n – l x_n, A x_n – l x_n) = (A x_n, A x_n) – 2 l (A x_n, x_n) + l ² (x_n, x_n) £
£ l ² – 2 l (A x_n, x_n) + l ² = 2 l (l – (A x_n, x_n) ) ® 0.

Предположим, что оператор A – l I имеет ограниченный обратный оператор. Тогда справедливо неравенство || x || £ c || (A – l I) x ||, c > 0. При подстановке в это неравенство последовательности x_n получаем противоречие, значит, оператор A – l I не имеет ограниченного обратного и l есть спектральное значение для оператора A. Теорема доказана.