Слабая сходимость. Рефлексивность

С помощью ограниченных линейных функционалов в банаховом пространстве вводится новый тип сходящихся последовательностей.

Определение 7.3. Будем говорить, что последовательность x_n точек банахова пространства X слабо сходится к точке x ₀ Î X (обозначается x_n ® x ₀), если для любого f Î X' выполнено f (x_n) ® f (x ₀).

Очевидно, что если последовательность x_n сходится к x ₀ по норме, то она сходится слабо. Действительно, | f (x_n) – f (x ₀) | = | f (x_n – x ₀) | £ || f || || x_n – x ₀ || ® 0.

Покажем на примере, что слабо сходящаяся последовательность может не сходится по норме.

Пример 7.5. В пространстве c ₀ последовательность 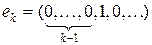по норме не сходится, так как || e_i – e_j || = 1 при i ¹ j. Покажем, что она сходится слабо. Действительно, любой функционал f Î (c ₀) ' представляется в ви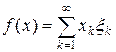де , где 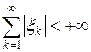. Тогда f (e_k) = x _k ® 0.

Введение слабой топологии мотивируется тем, что в ряде построений возникают последовательности, которые не сходятся по норме, но сходятся слабо, а также отображения, которые переводят слабо сходящиеся последовательности в слабо сходящиеся.

Пусть X – банахово пространство, X' – его сопряженное. Зафиксируем точку x ₀ Î X и f (x ₀) будем рассматривать как функцию от f. Получаем отображение 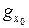из X' в R, 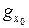: X' ' f ® f (x ₀) Î R, т. е. функционал 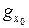, определенный на пространстве X'. Из соотношений

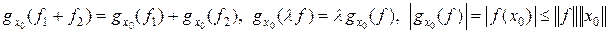
получаем, что функционал 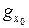линеен и ограничен, причем 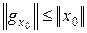, т. е. 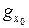Î (X') '. Согласно следствию 4.1 теоремы Хана – Банаха, существует функционал f ₀ такой, что f ₀ (x ₀) = || x ₀ || и || f ₀ || = 1. Поэтому

.

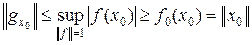Значит, 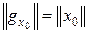. В результате получаем изометрическое отображение J : X ® (X') ', которое каждому x Î X ставит в соответствие функционал g_x из сопряженного пространства к X'. Как будет показано ниже на примерах, возможны случаи J X = X" и J X ¹ X".

Определение 7.4. Банахово пространство X называстся рефлексивным, если J X = X".

Поскольку J – инъективное отображение, то в случае рефлексивного пространства X J является биекцией между X и X". Это означает, в частности, что для сопряженного пространства X' справедлива следующая теорема об общем виде линейного ограниченного функционала: для любого ограниченного линейного функционала F на пространстве X' существует точка x ₀ Î X такая, что F представляется в виде F ( f ) = f (x ₀).

Пример 7.6. Пусть X = L_p [0, 1], 1 < р < + ¥, тогда, согласно теореме Рисса, (L_p [0, 1] ) ' @ L_q [0, 1] и ( (L_p [0, 1] ) ' ) ' @ L_p [0, 1], причем последний изоморфизм, построенный с помощью теоремы Рисса, совпадает с отображением J, построенным выше. Таким образом, пространство L_p [0, 1] при 1 < р < + ¥ является рефлексивным.

Пример 7.7. Пусть c ₀ – пространство последовательностей x = { x_k } таких, что x_k ® 0 с нормой .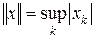

Как показано в разделе 5.3, (c ₀) ' @ l ₁ и (l ₁) ' @ l _¥, причем отображение J : c ₀ ® l _¥ является естественным вложением, но c ₀ ¹ l _¥. Значит, пространство c ₀ нерефлексивно.

Пример 7.8. Пространство C [0, 1] также не является рефлексивным. Сопряженное пространство к C [0, 1] есть пространство функций ограниченной вариации, полунепрерывных слева и таких, что g (0) = 0, или, что эквивалентно, – пространство зарядов на борелевском кольце. Можно показать, что линейный ограниченный функционал F Î (C [0, 1] ) " вида 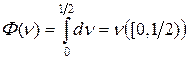не может быть представлен в виде 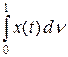с непрерывной функцией x.

В случае рефлексивных банаховых пространств справедлив ряд теорем, которые для произвольных банаховых пространств могут оказаться неверными. Часто доказательства в случае рефлексивных пространств упрощаются. Сформулируем некоторые такого рода результаты.

Если X – рефлексивное банахово пространство и A : X ® X – оператор, то (A' ) ' = A. Действительно, для функционала F Î X" найдется точка x ₀ Î X такая, что F ( f ) = f (x ₀) для всех f Î X' и

.

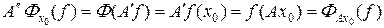Последняя запись означает, что A" переводит функционал, соответствующий точке x ₀, в функционал, соответствующий точке A x ₀, т. е. A" действует так же, как A. Отсюда получаем, например, что в теореме 6.2 и ее следствиях (следствия 6.1 – 6.3) можно поменять местами оператор A и A'. Получаем следующую теорему.

Теорема 7.4. Пусть X – рефлексивное банахово пространство, A Î L (X, X). Тогда 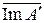совпадает с (Ker A ) ^{^} – множеством функционалов f таких, что f (x) = 0, если A x = 0.

Отметим, что в нерефлексивных банаховых пространствах теорема 7.4 неверна. Действительно, пусть X = L ₁ [0, 1] и оператор A : L ₁ [0, 1] ® L ₁ [0, 1] задан формулой 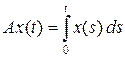. Тогда Ker A = {0} и, следовательно, (Ker A ) ^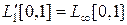{^} =. Вычислим действующий в L _¥ [0, 1] сопряженный оператор A':

,

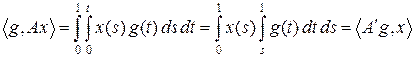т. е. .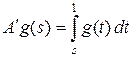

Таким образом, Im A' состоит из функций f (s), удовлетворяющих условию Липшица и обращающихся в нуль в точке s = 1. Это множество отстоит от функции f ₀ (s) º 1 Î L _¥ [0, 1] на расстояние 1 и, следовательно, неплотно в L _¥ [0, 1].