Уравнения с компактными операторами. Фредгольмовы операторы

При исследовании интегральных уравнений 2-го рода Э. Фредгольм получил ряд теорем, заведомо не имеющих места для произвольных уравнений. В дальнейшем Ф. Рисс и Ю. Шаудер показали, что особые свойства этого класса уравнений вытекают из компактности интегральных операторов, и построили общую теорию уравнений с компактными операторами.

Пусть X – банахово пространство, K : X ® X – компактный линейный оператор. Рассматриваются четыре уравнения: два в пространстве X

x – K x = y, (7)

x – K x = 0 (8)

и два в пространстве X', сопряженном к X

f – K' f = g, (9)

f – K' f = 0. (10)

Напомним, через Ker (I – K) мы обозначаем пространство решений уравнения (8), Im (I – K) – множество y, для которых уравнение (7) имеет решение. Следующие теоремы устанавливают связи между уравнениями (7) – (10).

Теорема 8.6. Если K – компактный оператор, то пространства Ker (I – K) и Ker (I – K') конечномерны, a Im (I – K) и Im (I – K') замкнуты.

Доказательство. На подпространстве Ker (I – K) имеем K x = x, т. е. оператор K действует как тождественный. Но тождественный оператор является компактным только в случае конечномерного пространства. Значит, Ker (I – K) конечномерно.

Так как K' – компактный оператор, то приведенное выше рассуждение относится и к Ker (I – K').

Обозначим L = Ker (I – K). Согласно теореме 4.5, существует разложение в прямую сумму X = L Å M. Обозначим через B сужение оператора A = I – K на M. Если B x = 0, то x Î M Ç L и, значит, x = 0. Таким образом, Ker B = {0}, т. е. B – инъективный оператор; по построению Im B = Im A. Значит, существует обратный оператор B ^{– 1} : Im A ® M. Покажем, что оператор B ^{– 1} ограничен. Предположим противное. Тогда существует последовательность x_n Î M такая, что || A x_n || ® 0 и || x_n || = 1. Так как последовательность { x_n } ограничена, то { K x_n } – предкомпактное множество и, значит, существует подпоследовательность 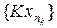, которая сходится в M к точке x ₀. Но тогда 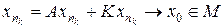. В силу непрерывности A имеем 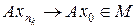и так как 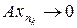по условию, то A x ₀ = 0. Значит, x ₀ Î L Ç M, т. е. x ₀ = 0. Но так как 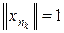, получаем противоречие. Таким образом, оператор B ^{– 1} ограничен, т. е. справедлива оценка

|| x || £ c || B x || " x Î M. (11)

Из оценки (11) получаем замкнутость образа Im A. Пусть y_n = A x_n – последовательность элементов из Im A и y_n ® y ₀. Покажем, что y ₀ Î Im A. Из неравенства (11) получим || x_n – x_m || £ c || A x_n – A x_m || = c || y_n – y_m || ® 0, n, m ® ¥, т. е. { x_n } – последовательность Коши. Пространство X полнoe, значит, x_n ® x ₀. Тогда, переходя к пределу, получаем y ₀ = A x ₀, т. е. y ₀ Î Im A. Так как K' – компактный оператор, то предыдущее рассуждение справедливо для оператора I – K'. Теорема доказана.

Следствие 8.3. Уравнение (7) разрешимо для данного y Î X тогда и только тогда, когда f (y) = 0 для любого функционала f, удовлетворяющего уравнению (10).

Доказательство вытекает из утверждения о замкнутости образа Im A и теоремы 6.2.

Определение 8.3. Пусть X и Y – банаховы пространства. Оператор A Î L (X, Y) называется фредгольмовым, если 1) dim Ker A < + ¥; 2) dim Ker A' < + ¥; 3) образ Im A замкнут.

Таким образом, теорема 8.6 утверждает, что оператор вида I – K, где K – компактный оператор в банаховом пространстве, является фредгольмовым.

Важной характеристикой фредгольмова оператора A является его
индекс

ind A = dim Ker A – dim Ker A'.

В случае конечномерных пространств X и Y имеем dim Ker A = dim X – r, dim Ker A' = dim Y – r, где r – ранг матрицы, задающей оператор A. Тогда ind A = dim X – dim Y. В частности, если A : X ® X и X конечномерно, то ind A = 0. Если фредгольмов оператор A действует в бесконечномерном пространстве X, то его индекс может быть ненулевым. Например, для оператора одностороннего левого сдвига V : l ₂ ® l ₂, действующего по формуле V (x) = (x ₂, x ₃, ¼), имеем Ker V = {(x ₁, 0, ¼)} и dim Ker V = 1. Но Im V = l ₂ и по следствию 6.3 теоремы 6.2 Ker V' = {0}. Значит, ind V = 1.

Теорема 8.7. Если K – компактный оператор в банаховом пространстве X, то ind (I – K) = 0.

Рассмотрим сначала некоторые свойства фредгольмовых операторов, из которых теорема 8.7 получается как простое следствие.

Пусть банаховы пространства X и Y разложены в прямые суммы своих замкнутых векторных подпространств X = X ₁ Å X ₂ и Y = Y ₁ Å Y ₂ и P_i : X ® X_i, Q_i : Y ® Y_i, i = 1, 2, – соответствующие проекторы (см. пример 2.4). Ограниченному линейному оператору A : X ® Y можно поставить в соответствие операторную матрицу 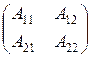, где A_{i j} Î L (X_i, Y_j), A_{i j} = Q_i A, i, j = 1, 2. При этом оператор A действует на пару (x ₁, x ₂), где x ₁ Î X ₁, x ₂ Î X ₂, как обычное умножение матрицы на вектор:

A (x ₁, x ₂) = (A ₁₁ x ₁ + A ₁₂ x ₂, A ₂₁ x ₁ + A ₂₂ x ₂),

и произведению операторов соответствует произведение матриц, определенное по тому же правилу, что и для числовых матриц.

Если оператор A задается с помощью диагональной матрицы 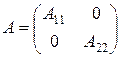, то оператор A фредгольмов тогда и только тогда, когда операторы A ₁₁ и A ₂₂ являются фредгольмовыми. Действительно, Ker A = Ker A ₁₁ Å Ker A ₂₂, Ker A' = Ker A' ₁₁ Å Ker A' ₂₂, Im A = Im A ₁₁ Å Im A ₂₂, откуда следует утверждение и равенство ind A = ind A ₁₁ + ind A ₂₂.

Если оператор A фредгольмов, а оператор B имеет ограниченный обратный, то оператор B A фредгольмов и ind A = ind B A. Действительно, в силу обратимости оператора B пространство Ker B A = Ker A, Ker (B A) ' = B' (Ker A' ), dim Ker (B A) ' = dim Ker A', подпространство Im (B A) = B (Im A ) замкнуто.

Пусть оператор A : X ® Y фредгольмов. Обозначим X ₁ = Ker A, X ₂ – дополнение к X ₁, которое существует в силу теоремы 4.5. Подпространство Im A замкнуто и по теореме 6.2 Im A = (Ker A' ) ^{^}. Так как ядро Ker A' конечномерно, подпространство Y ₂ = Im A может быть задано с помощью конечного числа линейно независимых функционалов, то по теореме 4.5 существует конечномерное дополнение Y ₁ для пространств Y ₂ и dim Y ₁ = dim Ker A'. При этом разложении пространств X = X ₁ Å X ₂ и Y = Y ₁ Å Y ₂ оператор A задается матрицей 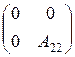, причем оператор A ₂₂ обратим и ind A = dim X ₁ – dim Y ₁.

Пусть при том же разложении пространств некоторый ограниченный оператор C : X ® Y записывается в виде

,

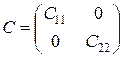где C ₂₂ – обратимый оператор. Тогда C – фредгольмов оператор и ind C = ind C ₁₁ + ind C ₂₂ = ind C ₁₁ = dim X ₁ – dim Y ₁ = ind A.

Теорема 8.8. Если A – фредгольмов оператор, то существует число d > 0 такое, что любой оператор B, удовлетворяющий условию || A – B || < d, фредгольмов и ind A = ind B.

Доказательство. Пусть по фредгольмову оператору A построено разложение пространств X и Y, описанное выше, при котором оператору A соответствует матрица 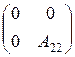, где A ₂₂ – обратимый оператор. При том же разложении пространств оператору B соответствует матрица 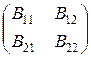. Если 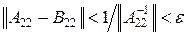, то, согласно теореме 2.3, оператор B ₂₂ обратим. Так как 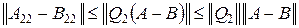, получаем, что если d = e / || Q ₂ ||, то из условия || A – B || < d следует обратимость оператора B ₂₂. Матрицы 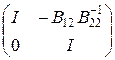и 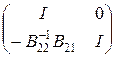задают обратимые операторы. Перемножая матрицы, получаем равенство

,

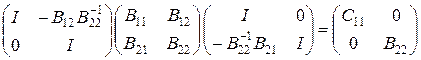где .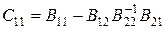

Так как оператор 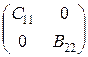фредгольмов и при умножении на обратимые операторы фредгольмов оператор переходит в фредгольмов и индекс не меняется, получаем, что оператор B фредгольмов и ind B = ind A. Теорема доказана.

Доказательство теоремы 8.7. Рассмотрим семейство операторов A_t = I – t K, 0 £ t £ 1. По теореме 8.6 все эти операторы фредгольмовы. Согласно теореме 8.8, функция j (t) = ind (I – t K) непрерывна на [0, 1]. Но j (0) = ind I = 0. Если j (1) = ind (I – K) ¹ 0, то функция j (t) должна принимать все промежуточные значения, что невозможно, так как j (t) принимает только целые значения. Значит, j (t) º 0, что и требовалось доказать.

Следствие 8.4. Уравнения (8), (10) имеют одинаковое число линейно независимых решений.

Это другая формулировка утверждения о том, что ind A = 0.

Следствие 8.5. Уравнение (7) разрешимо для любой правой части тогда и только тогда, когда однородное уравнение (8) имеет только нулевое решение.

Доказательство. Пусть уравнение (8) имеет только нулевое решение. По следствию 8.5 уравнение (10) имеет только пулевое решение. Тогда условие разрешимости из следствия 8.3 теоремы 8.6 выполнено для любого y Î X, т. е. уравнение (7) разрешимо для любого y.

Если уравнение (7) разрешимо для любого y Î X, то, согласно следствию 6.3 теоремы 6.2, Ker A' = {0}. Тогда по теореме 8.7 и Ker A = {0}. Следствие доказано.

Следствие 8.6. Сопряженное уравнение (9) разрешимо для данного g Î X' тогда и только тогда, когда g (x) = 0 для любого x, являющегося решением однородного уравнения (8).

Доказательство. Уравнение f – K' f = g есть уравнение с компактным оператором, и поэтому применимы теоремы 8.6 и 8.7. Условие разрешимости уравнения (9) есть F (g) = 0 для любого F Î X", удовлетворяющего уравнению F – K" F = 0. Если X – рефлексивное банахово пространство, то это уравнение совпадает (с точностью до изоморфизма J : X ® X" ) уравнением (8).

Если пространство X нерефлексивно, то, вообще говоря, уравнение
F – K" F = 0 рассматривается в более широком пространстве и может иметь больше решений, чем уравнение (8). Но, согласно теореме 8.7, имеем dim Ker (I – K) = dim Ker (I – K') = dim Ker (I – K"). Поскольку Ker (I – K) Ì Ker (I –
– K"), то из совпадения размерностей имеем Ker (I – K) = Ker (I – K"). Следствие доказано.

Результаты, полученные в теоремах 8.6 и 8.7, легко распространить на несколько более широким класс уравнений.

Теорема 8.9. Пусть X и Y – банаховы пространства и оператор A : X ® Y имеет вид A = A ₁ + K, где A ₁ – обратимый оператор, K – компактный оператор. Тогда оператор A фредгольмов и ind A = 0.

Доказательство. Оператор A можем представить в виде 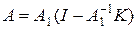. Оператор 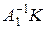компактный, оператор 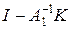фредгольмов и 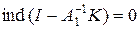. Как уже отмечалось, при умножении фредгольмова оператора на обратимый получается фредгольмов оператор с тем же индексом. Значит, A – фредгольмов оператор и ind A = 0.