Проверка статистических гипотез

Расчет коэффициента корреляции

Таблица 3.7

№ п/п	xi	yi	xi 2	yi 2	xiyi
	4,6 4,6 4,7 4,8 4,8 4,8 4,9 4,9 4,9 5,0	12,4 12,7 13,0 13,3 13,1 13,2 13,5 13,5 13,6 13,7	21,16 21,16 22,09 23,04 23,04 23,04 24,01 24,01 24,01 25,00	159,76 161,29 169,00 176,89 171,61 174,24 182,25 182,25 184,96 187,69	57,04 58,42 61,10 63,84 62,88 63,66 66,15 66,15 66,64 68,50
Сумма	48,0	132,0	230,56	1743,94	634,08

По формуле (3.7) вычисляем коэффициент корреляции:

r = 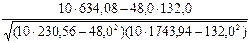» 0,967.

Такое значение коэффициента корреляции свидетельствует о наличии сильной положительной корреляции между полученными результатами.

Ответ: 0,967.

Статистической гипотезой (или просто гипо­тезой) называется утверждение о распределении генеральной совокупности, соответ­ствующее некоторым представлениям об изучаемом явлении. В частном случае это может быть утверждение о значениях параметров (a и s) нормально распределенной генеральной совокупности.

Предположим, что в эксперименте участвуют две группы школьников. Одна из них (контрольная) обучается по традиционной программе, а для второй (эксперименталь­ной) используется новые специальные методики обучения. Действенность новых ме­тодик оценивается по различию результатов, показанных в этих группах после опре­деленного периода обучения. Например, по полученным данным можно проверить справедливость следующих утверждений (гипотез):

1. Среднее значение результатов не изменилось, т.е. a ₁ = a ₂, где a ₁ и a ₂ - средние значения соответствующих генеральных совокупностей (результатов школьников, которые обучавшихся по традиционной (a ₁) и новой (a ₂) программам).

2. Вариативность результатов возросла: s₂ > s₁. Здесь s₁ и s₂ – значения стандарт­ных отклонений соответствующих генеральных совокупностей.

3. Средний результат возрос на 0,3 балла: a ₂ - a ₁ = 0,3.

Гипотезы проверяют с помощью определенного метода, который принято называть критерием. При этом обычно рассматривают две генеральные совокупности, одна из которых может представлять собой теоретическую модель (например, нормальное распределение), а о второй судят по выборке из нее. В других случаях обе генераль­ные совокупности представлены выборками.

Первоначально гипотезу всегда можно сформулировать таким образом: между двумя генеральными совокупностями нет ожидаемого различия. Такая гипотеза назы­вается нулевой гипотезой, или нуль-гипотезой. Обратное ей утверждение о том, что в действительности между генеральными совокупностями есть различия, называется альтернативной гипотезой, или альтернативой. Нулевую гипотезу принято обозна­чать, как H ₀, а альтернативную - H ₁. Пусть, например, оценивается эффективность но­вой методики обучения по среднему значению результата в контрольной и экспери­ментальной группах. Тогда нулевую гипотезу H ₀ можно сформулировать так: среднее значение результатов не изменилось, т.е. a ₁ = a ₂. Для краткости это записывается так: H ₀: a ₁ = a ₂. Если заранее нельзя сказать, к какому результату приведет новая мето­дика, то альтернативная гипотеза H ₁ будет состоять в том, что среднее значение гене­раль­ных совокупностей неодинаковы: H ₁: a ₁ ¹ a ₂.

Ошибки, допускаемые при проверке гипотез, удобно разделить на два типа: 1) от­клонение гипотезы H ₀, когда она верна, - ошибка первого рода; 2) принятие гипотезы H ₀, когда в действительности верна какая-то другая гипотеза, - ошибка второго рода. Вероятность ошибки первого рода обозначается α. Величина α называется уровнем значимости критерия, по которому проверяется справедливость гипотезы H ₀.

Любая гипотеза должна формулироваться, а уровень значимости задаваться иссле­дователем всегда до получения экспериментальных данных, по которым эта гипотеза будет проверяться.

При выборе уровня значимости обычно исходят из практических соображений, от­вечая на вопрос: какую вероятность ошибки будем считать допустимой для конкрет­ной задачи? Обычно считают достаточным α = 0,05 (5%), иногда α = 0,01, редко α = 0,001.

Если необходимо проверить гипотезу о том, что две независимые выборки полу­чены из генеральных совокупностей X и Y с одинаковыми дисперсиями s _х ² и s _y ², то можно использовать F-критерий Фишера.

Условия применения F -критерия: обе выборки независимы и получены из нор­мально распределенных генеральных совокупностей с параметрами a_x, s _x и a_y, s _y.

Гипотеза H ₀: s _x ² = s _y ².

Альтернативна H ₁: s _x ² ¹s _y ².

Уровень значимости критерия задается α.

Порядок применения F - критерия следующий:

1. Применяется предположение о нормальности распределения генеральных сово­купностей, формулируется гипотеза и альтернатива, назначается уровень значимости α, как указано выше.

2. Получают две независимые выборки из совокупностей Х и Y объемом n_x и n_y со­ответственно.

3. Рассчитывается значение дисперсий D_x и D_y. Большую из дис­персий (D_x или D_y) обозначают S ₁, меньшую - S ₂.

4. Вычисляется значение F - критерия по формуле:

F = 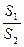. (3.8)

5. Сравнивается вычисленное значение F с критическим значением F-критерия при заданном уровне значимости α и числе степеней свободы t ₁ = n ₁-1 и t ₂ = n ₂-1. Критиче­ские значения F при уровнях значимости α, равных 0,05, 0,01, 0,001 приведены в таб­лице 5 Приложения.

Отметим, если цель исследования доказать, что одна дисперсия больше другой (H ₁: s₁² > s₂²), то критические значения берутся непосредственно из этой таблицы. Если же рассматривается гипотеза H ₁: s₁² ¹ s₂²), то критические значения, взятые из таблицы 5 Приложения, соответствуют удвоенным уровням значимости: 0,01, 0,02 и 0,002.

6. Делается вывод: если вычисленное значение F -критерия больше или равно кри­тическому, то дисперсии различаются значимо на заданном уровне значимости. В противном случае нет оснований для отклонения нулевой гипотезы о равенстве двух дисперсий.

Пример 3.18. Одна группа школьников (n ₁=21) третьих классов взята из обычной школы, а другая (n ₂=11) - из школы со специальной математической подготовкой. В обеих группах известны резуль­таты тестирования по изученным темам. Предстоит проверить утверждение о том, что по вариатив­ности результатов школьники при обеих системах подготовки не отличаются.

Решение. Действуем в порядке, указанном выше.

1. Гипотеза H ₀: s _x ² =s _y ², альтернатива H ₁: s _x ² ¹ s _y ² (поскольку заранее не уверены в том, что какая-либо из генеральных дисперсий больше другой). Задаем уровнем значимости α = 0,02 для того, чтобы воспользоваться данными таблицы 5 Приложения.

Принимаем предположение о нормальности распределения обеих генеральных совокупностей. (Как можно обосновать такое предположение показано в следующем примере).

2-3. Пусть рассчитанные выборочные стандартные отклонения результатов составили: D_x = 10,89, D_y = 2,89. Обозначаем S ₁ = D_x = 10,89, S ₂ = D_y = 2,89.

4. Вычисляем значение F -критерия по формуле (3.8): F =10,89/2,89 = 3,77.

5. Из таблицы 5 Приложения при α=0,02; t ₁ = n ₁-1 = 21-1 = 20 и t ₂ = n ₂ - 1 = 10 находим F _0,02 = 4,4.

6. Вывод: поскольку F < F _0,02, то на уровне значимости α = 0,02 различие дисперсий статистически незначимо, т.е. можно считать, что школьники при обеих системах подготовки не отличаются по признаку вариативности результатов.

Хотя наблюдаемое в эксперименте различие дисперсий и кажется большим, но имеющиеся статистические данные не дают оснований для отклонений гипотезы о том, что для гене­ральных совокупностей (всех школьников третьих классов обычных школ и школ с углубленной ма­тематической подготовкой) дисперсии (а значит, и стандартное отклонение) различаются на уровне значимости 0,02.

При решении целого ряда педагогических задач исследователь всякий раз предпо­лагает, что случайная величина распределена по определенному закону (чаще всего предполагают, что она распределена по нормальному закону распределения). В мате­матической статистике разработаны специальные критерии – критерии согласия, с помощью которых можно оценить вероятность того, что полученная выборка не про­тиворечит сделанному предположению о виде закона распределения случайной вели­чины.

Наиболее распространенным критерием является критерий согласия c² («хи-квадрат») (критерий Пирсона), с помощью которого устанавливается степень соот­ветствия между статистическим материалом и выдвинутой гипотезой. Согласно кри­терию Пирсона, проверку гипотезы о характере распределения случайной величины проводят следующим образом:

1. Формулируется гипотеза, выбирается уровень значимости α.

2. Исходный статистический ряд, объем выборки которого n ³40, представляют в виде сгруппированного статистического ряда (k – число интервалов, n_i - частоты).

3. Оценивается опытное значение c² по формуле

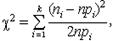
(3.10)

где p_i - вероятность попадания СВ в i -й интервал, значение которого вычислено для теоретического закона распределения.

4. Оценивается число степеней свободы «t»: t = k – r – 1, где r – число параметров теоретического закона распределения, оцененных по данной выборке.

5. По специальной таблице (таблицу 6 Приложения) определяем критическое зна­чение c_α² хи-квадрат критерия для уровня значимости α и числа степеней свободы t.

6. Ведется проверка условий. Если c² ³c_α², то отклонения статистического и теоре­тического законов распределения значимые, т.е. данные опыта противоречат сделан­ному предположению о виде закона распределения; в противном случае (c²<c_α²) от­клонения не значимые, т.е. данные опыта не противоречат сделанному предположе­нию о виде закона распределения.

Пример 3.19. В ходе дидактического эксперимента проводился итоговый контроль знаний уча­щихся по специальному тесту, включающему 20 контрольных вопросов. В эксперименте участвовало 200 учеников. Экспериментальные данные по итоговому контролю знаний представлены в таблице 3.8, где i - номер интервала, x_i и x_{i +1} - границы интервала, n_i – число учеников, правильно ответивших на x_i * контрольных вопросов, т.е. n_i - число учеников, попавших в i -й интервал. Требуется оценить с помощью критерия c² гипотезу о согласии выборочного распределения при заданном уровне значи­мости α = 0,05.

Решение.

1. По данным таблицы 3.8, используя формулы (3.2) и (3.5), определяем значения` x и s:` x = 9,72, s=3.81.

2. Вычисляем теоретические вероятности p_i правильного ответа на x_i ^* контрольных вопросов по формуле (6.3) (здесь a =` x):

P (x_i < x_i ^*< x_{i +1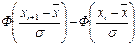}) = или

P (x_i < x_i ^*< x_{i +1}) = Ф(z_{i +1}) – Ф(z_i) при.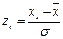

Далее, при расчете значений p_i заменяем наименьшую величину z_i = z ₁, равную z ₁ = -2,58 (при x ₀=0,` x =9,72, s=3,81) на -¥, а наибольшую величину z<sub>i</sub> = z <sub>11</sub>, равную z <sub>11</sub>=2,71 (при x <sub>20</sub>=20,` x =9,72 и s = 3,81), на +¥. Значения функции Ф(z) находим по таблице 4 Приложения. Результаты вычислений сводим в таблицу 3.9.